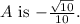Question

Given cos A = 3/ sqrt 10
and cot A = -3, determine the value of sin A in radical form.

Answer 1

The value of sin A in radical form is:

`\[ \sin A = -(√(10))/(10) \]`

Step-by-step explanation:

The given information includes
`\( \cos A = (3)/(√(10)) \) and \( \cot A = -3 \). To determine \( \sin A \),` we can use the identity
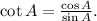`\( \cot A = (\cos A)/(\sin A) \).` Substituting the given values, we get
`\( -3 = ((3)/(√(10)))/(\sin A) \).`

To isolate
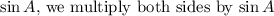`\( \sin A \), we multiply both sides by \( \sin A \)`and simplify, resulting in
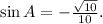`\( \sin A = -(√(10))/(10) \).` The negative sign indicates that
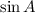`\( \sin A \)`is negative, placing the angle in the third quadrant where both sine and cosine are negative.

In the third quadrant, the cosine is negative and the sine is also negative. Therefore,
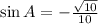`\( \sin A = -(√(10))/(10) \)`. This means that the ratio of the opposite side to the hypotenuse in the right triangle formed by angle
`\( A \) is \(-(√(10))/(10)\).`

Answer 2

We can use the definitions of cosine and cotangent to find the value of sin A.

cos A = adjacent/hypotenuse = 3/√10

cot A = adjacent/opposite = -3

We can use the Pythagorean theorem to find the value of the opposite side of the triangle:

a^2 + b^2 = c^2

3^2 + b^2 = 10

b^2 = 1

b = 1

So the opposite side is 1.

Now we can use the definition of cotangent to find the adjacent side:

cot A = adjacent/opposite

-3 = adjacent/1

adjacent = -3

Now we can use the Pythagorean theorem to find the value of the hypotenuse:

a^2 + b^2 = c^2

(-3)^2 + 1^2 = c^2

9 + 1 = c^2

c^2 = 10

c = √10

So the hypotenuse is √10.

Finally, we can use the definition of sine to find the value of sin A:

sin A = opposite/hypotenuse = 1/√10

Therefore, the value of sin A in radical form is 1/√10.