Question

Using the formula for the volume of a cone,
express r in terms of V, h, and

Answer 1

`\sqrt{(3V)/(\pi h) }=r`

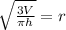
Explanation:

The formula for volume of a cone is V = 1/3πr^2h, where V is the volume, r is the radius, and h is the height.

We can express r in terms of the other three parts of the formula by isolating it:

`V=1/3\pi r^2h\\\\3V=\pi r^2h\\\\(3V)/(h\pi )=r^2\\ \\\sqrt{(3V)/(h\pi ) }=r^`

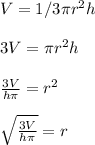
We can check first by choosing a value for r and h, which will allow us to find a volume. Then, we can rearrange the numbers using the formula expressing r in terms of the volume, height, and pi

For example, using a radius that is 2 units and height that is 5
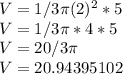`V=1/3\pi (2)^2*5\\V=1/3\pi *4*5\\V=20/3\pi \\V=20.94395102` units will give a volume of 20/3π (i.e., 20.94395102) units:

Now, we can plug in our numbers for the formula expressing r in terms of volume, height, and pi and check that we get a radius of 2:

`\sqrt{((3*20/3\pi )/(5\pi )) } =2\\\sqrt{((20\pi )/(5\pi )) }=2\\ √(4)=2\\ 2=2`

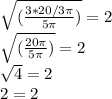
Thus, our formula expressing r in terms of V, h, and π is correct