Question

The table shows the number of rabbits r in a particular forest t years after a forest fire. Write and use an exponential model to find how many years it will take for the rabbit population to surpass 20,000. Please show your work!​

Answer 1

t = 6.29 years

Explanation:

The general formula of an exponential function is

`y=ab^x`, where a is the initial value (i.e., value of y when x = 0), b is the base, and x is the exponent.

We can express rabbit population as a function of time in years, which means in our formula, r is like y and t is like x:

`r=ab^t`

Because at time t = 0, the rabbit population is 20, we know that our a value for the equation is 20.

We can find b by simply plugging in 20 for a and any point for r and t like (1, 60):

`60=20b^1\\3=b`

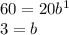
Thus, the equation we will need to use to find the rabbit population is

`r < 20(3)^t`

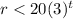
It's helpful to use an inequality where the equation is greater than r since we want to know how many years it will take for the population to exceed 20000:

`20000 < 20(3)^t\\\\1000 < 3^t\\\\log(1000) < log(3)^t\\\\log(1000) < t*log(3)\\\\log(1000)/log(3) < t\\\\6.287709823 < t\\6.29 < t`

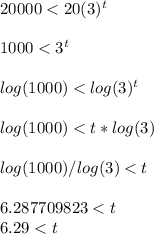
We can check our answer by plugging in 6.29 for t and check whether the answer we get is greater than 20000:

`20000 < 20(3)^6^.^2^9\\20000 < 20*1002.519185\\20000 < 20050.38369\\20000 < 20050.38`