Question

The mass of one small ball is 1.50 g, and the mass of another is 870.0 g. If the center-to-center distance between these two balls is 10.0 cm, find the magnitude of the gravitational force that each exerts on the other.

Answer 1

Approximately
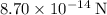`8.70 * 10^(-14)\; {\rm N}`, assuming that both balls are of uniform density.

Step-by-step explanation:

The gravitational attraction between two spheres of uniform density is:

`\begin{aligned}F &= (G\, M\, m)/(r^(2))\end{aligned}`,

Where:

• 
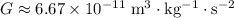  `G \approx 6.67 * 10^(-11)\; {\rm m^(3) \cdot kg^(-1) \cdot s^(-2)}}` is the gravitational constant,
• 
  `M` and
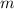  `m` are the mass of the two spheres, and
• 
  `r` is the distance between the center of the two spheres.

Apply unit conversion and ensure that mass and distance are both measured in standard units:

`\displaystyle m = 1.50\; {\rm g} * \frac{1\; {\rm kg}}{10^(3)\; {\rm g}} = 1.50 * 10^(-3)\; {\rm kg}`.

`\displaystyle M = 870.0\; {\rm g} * \frac{1\; {\rm kg}}{10^(3)\; {\rm g}} = 0.8700\; {\rm kg}`.

`\displaystyle r = 10.0\; {\rm cm} * \frac{1\; {\rm m}}{100\; {\rm cm}}= 0.100\; {\rm m}`.

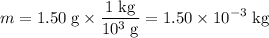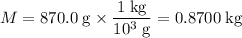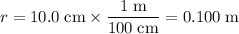Substitute these value into the equation and evaluate:

`\begin{aligned}F &= (G\, M\, m)/(r^(2)) \\ &= \frac{(6.67 * 10^(-11)\; {\rm m^(3)\cdot s^(-1)\cdot kg^(-2)})\, (0.8700\; {\rm kg})\, (1.50* 10^(-3)\; {\rm kg})}{(0.100\; {\rm m})^(2)} \\ &= ((6.67 * 10^(-11))\, (0.8700)\, (1.50* 10^(-3)))/((0.100)^(2))\; {\rm kg\cdot m\cdot s^(-2)} \\ &= ((6.67 * 10^(-11))\, (0.8700)\, (1.50* 10^(-3)))/((0.100)^(2))\; {\rm N} \\ &\approx 8.70 * 10^(-14)\; {\rm N}\end{aligned}`.