Question

For the titration of 50. mL of 0.10 M ammonia with 0.10 M HCl, calculate the pH. For ammonia, NH3, Kb = 1.8 x 10-5.

(a) Before the addition of any HCl solution. pH = the tolerance is +/-1 in the 4th significant digit

(b) After 20. mL of the acid has been added. pH = the tolerance is +/-1 in the 3rd significant digit

(c) After half of the NH3 has been neutralized. pH = the tolerance is +/-1 in the 3rd significant digit

(d) At the equivalence point. pH = the tolerance is +/-1 in the 3rd significant digit

Answer 1

(a)

Before the addition of any acid, we just treat this as a weak base problem, dealing with just the ionization of the weak base ammonia.

The ionization of ammonia is expressed by this reaction:

NH₃(aq) + H₂O(l) ⇄ OH⁻(aq) + NH₄⁺(aq)

We can set up an ICE table to show the initial concentration of each reactant and product, the change in concentration, and the concentration of all at equilibrium.

⇒NH₃(aq) + H₂O(l) ⇄ OH⁻(aq) + NH₄⁺(aq)

I 0.1 0 0

C -x +x +x

E 0.1 -x x x

(note that water is a liquid and therefore has no concentration)

We know that
`k_b = ([products])/([reactants])` and we know the value of kb given, so

`1.8*10^(-5)=(x^2)/(0.1-x)`

We could just solve for x from here, however that would end up being a quadratic equation which are annoying.

Since ammonia is a weak base, we can assume the amount of ammonia used (x) will be a negligible amount, and drop the -x from 0.1-x.

The statement now becomes

`1.8*10^(-5)=(x^2)/(0.1)\\x= 0.00134`

So, the concentration of OH⁻ = 0.00134 M

We can find the pOH from this, as pOH = -log([OH⁻])

pOH = -log(0.00134) = 2.872

pH = 14-pOH = 11.1

So, pH = 11.13

(b)

Before the equivalence point (when moles of base equal the moles of added acid), we are dealing with a buffer solution and can treat it as such.

The equation we will use is

NH₃(aq) + H₃O⁺(aq) → NH₄⁺(aq) + H₂O

After 20 ml of 0.1 M HCl has been added, 0.002 moles of HCl have been added.

There are two ways to do this, and I will do both.

Here I set up a mole table showing the moles of each reactant and product before and after reaction.

The H⁺ ions are given by the acid, so the moles of H⁺ will equal moles of acid.

⇒ NH₃(aq) + H⁺(aq) → NH₄⁺(aq)

before 0.005 0.002 0

after 0.003 0 0.002

H⁺ is the limiting reactant, so H⁺ will be completely used up and the remaining moles of NH₃ will be subtracted by that amount and NH₄⁺ will be produced by that amount.

From here, you must choose which method to do. Personally I find method 2 easier.

METHOD 1

Returning to this equation:

NH₃(aq) + H₂O(l) ⇄ OH⁻(aq) + NH₄⁺(aq)

we can plug in the new initial value of NH₄⁺ gotten from the reaction between NH₃(aq) and H⁺(aq). Set up another ICE table with this new initial concentration. NOTE that we have 0.002 moles of NH₄⁺ and 0.005 moles of NH₃ initially, but that is not concentration. We have to put these values over the new volume (0.02 + 0.05 ) to find concentrations.

⇒NH₃(aq) + H₂O(l) ⇄ OH⁻(aq) + NH₄⁺(aq)

I 0.0429 0 0.0286

C -x +x +x

E 0.0429 -x x 0.0286+x

`k_b = ([products])/([reactants])`

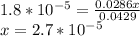`1.8*10^(-5)=(0.0286x)/(0.0429)\\x=2.7*10^(-5)`again assuming the change in concentration of NH₃ is negligible.

pOH = -log(x) = 4.568

pH = 14 - pOH = 9.43

METHOD 2

With the moles of NH₃ and its conjugate acid, NH₄⁺, we can plug them into the Henderson-Hasselbalch equation since it is a buffer solution before it hits the equivalence point.

The Henderson-Hasselbalch equation is

`pH = pKa + log([A^-])/([HA])`

for an acid and

`pOH = pKb + log([BH^+])/([B])`

for a base, where B is the base and BH+ is its conjugate acid. While the equation uses the concentrations of each, we can just use moles.

note that pKb = -log(kb)

Since this is a base, we will use the second equation.

`pOH = -\log(1.8*10^(-5))+\log(0.002)/(0.003)\\pOH = 4.568`

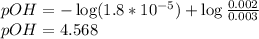
pH = 14 - pOH = 9.43

(c)

After half of the NH₃ is neutralized, that means we are halfway to the equivalence point. At halfway to the eq. point, pOH = pkb and pH = pka

So, pOH = -log(kb) = 4.74

pH = 14 - pOH = 9.26

(d)

At the equivalence point, moles of base and added acid are the same.

⇒ NH₃(aq) + H⁺(aq) → NH₄⁺(aq)

before 0.005 0.005 0

after 0 0 0.005

Only NH₄⁺ remains, so this is just a weak acid ionization problem.

Take the moles of NH₄⁺ and put it over the total volume--

Since we have 0.005 moles of 0.1 M HCl, we have 50 mL of HCl and 50 mL of NH₃, so 100 mL or 0.1 L total.

Another ICE table!

⇒ NH₄⁺(aq) + H₂O(l) ⇄ H₃O⁺(aq) + NH₃(aq)

I 0.05 M 0 0

C -x +x +x

E 0.05-x x x

Now to find ka.

ka*kb = kw

kw is a constant,
`1*10^(-14)`

So,

`(1*10^(-14))/(1.8*10^(-5))=k_a\\k_a=5.55*10^(-10)`

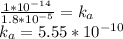
Back to the ice table.

`k_a = ([products])/([reactants])\\k_a = (x^2)/(0.05)\\`again, assuming the ionization of NH₄⁺ is negligible

Solving for x, we get x=5.270

x in this case is the concentration of H₃O⁺, so -log(x) = pH

pH = -log(5.270) = 5.28

Hope I could help!