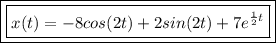Question

Solve using Laplace Transform. (if necessary, use partial fraction expansion). x' + 1/2 x = 17sin(2t), x(0) = -1

Answer 1

Use Laplace Transforms to solve the following differential equation.

`x'+(1)/(2)x=17sin(t); \ x(0)=-1`

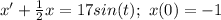
Take the Laplace transform of everything in the equation.

`L\{x'\}=sX-x(0) \Rightarrow \boxed{ sX+1}`

`L\{x\}=X \Rightarrow \boxed{ (1)/(2) X}`

`L\{sin(at)\}=(a)/(s^2+a^2) \Rightarrow 17(2)/(s^2+4) \Rightarrow \boxed{(34)/(s^2+4) }`

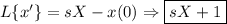
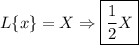
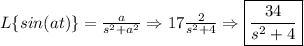
Now plug these values into the equation and solve for "X."

`\Longrightarrow sX+1+(1)/(2)X=(34)/(s^2+4) \Longrightarrow sX+(1)/(2)X=(34)/(s^2+4) -1 \Longrightarrow X(s+(1)/(2) )=(34)/(s^2+4) -1`

`\Longrightarrow X=(((34)/(s^2+4) -1))/((s+(1)/(2) )) \Longrightarrow \boxed{X=(-2(s^2-30))/((2s+1)(s^2+4))}`

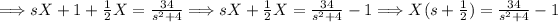
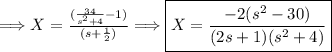
Now take the inverse Laplace transform of everything in the equation.

`L^(-1)\{X\}=x(t)`

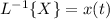
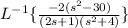`L^(-1)\{\((-2(s^2-30))/((2s+1)(s^2+4))\}` Use partial fractions to split up this fraction.

`[(-2(s^2-30))/((2s+1)(s^2+4))=(A)/(2x+1)+(Bs+C)/(s^2+4)] (2s+1)(s^2+4)`

`\Longrightarrow -2(s^2-30)=A(s^2+4)+(Bs+C)(2s+1)`

`\Longrightarrow -2s^2+60=As^2+4A+2Bs^2+Bs+2Cs+C`

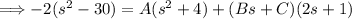
Use comparison method to find the undetermined coefficients A, B, and C.

For s^2 terms:

`-2=A+2B`

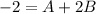
For s terms:

`0=B+2C`

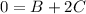
For #'s:

`60=4A+C`

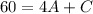
After solving the system of equations we get, A=14, B=-8, and C=4

`\Longrightarrow L^(-1)\{\((-2(s^2-30))/((2s+1)(s^2+4))\} \Longrightarrow L^(-1)\{ (-8s)/(s^2+4)+(4)/(s^2+4)+(14)/(2s+1) \}`

`\Longrightarrow L^(-1)\{ (-8s)/(s^2+4)+(4)/(s^2+4)+(14)/(2s+1) \}=-8cos(2t)+2sin(2t)+7e^{(1)/(2)t }`

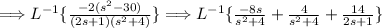
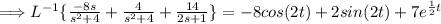
Thus, the DE is solved.

`\boxed{\boxed{x(t)=-8cos(2t)+2sin(2t)+7e^{(1)/(2)t }}}`