Answer:
Approximately
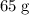 (assuming that the spring is horizontal, and that mass of the spring is negligible.)
(assuming that the spring is horizontal, and that mass of the spring is negligible.)
Step-by-step explanation:
In a simple harmonic motion, assuming that the mass is at position
 when time is
when time is
 , the position
, the position
 of the mass (the oscillator) at time
of the mass (the oscillator) at time
 would be:
would be:
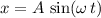 , where:
, where:
 is the amplitude of the motion, and
is the amplitude of the motion, and
 is the angular velocity of the motion.
is the angular velocity of the motion.
Note that
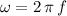 where
where
 is the frequency of the motion. It is given that
is the frequency of the motion. It is given that
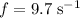 in this question.
in this question.
Differentiate
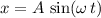 with respect to time
with respect to time
 to find the velocity of the oscillator at time
to find the velocity of the oscillator at time
 :
:
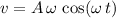 .
.
Differentiate again to find the acceleration of the oscillator:
 .
.
Let
 denote the mass of the oscillator and assume that mass of the spring is negligible. Assuming that the spring is horizontal, since all other force on the spring are balanced, the net force on the mass would be equal to the restoring force from the spring. By Newton's Laws of Motion, this net force would be:
denote the mass of the oscillator and assume that mass of the spring is negligible. Assuming that the spring is horizontal, since all other force on the spring are balanced, the net force on the mass would be equal to the restoring force from the spring. By Newton's Laws of Motion, this net force would be:
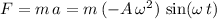 .
.
Divide the restoring force (which is equal to the net force) by displacement to find an expression for the spring constant:
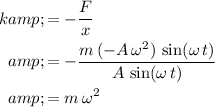 .
.
Since
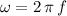 , this equation becomes:
, this equation becomes:
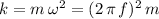 .
.
Rearrange this equation to find mass
 :
:
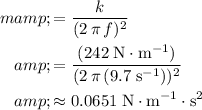 .
.
Note that
 . Hence:
. Hence:
 .
.
Apply unit conversion and round to the nearest gram:
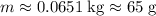 .
.