Question

Find the limit, or show that it does not exist.


`\[\lim_(x\to \infty) \] \left((1-x^2)/(x^3-x+1)\right)`

Answer 1

Find the following limit...

`\lim_(x \to \infty) ((1-x^2)/(x^3-x+1) )`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`\Longrightarrow \lim_(x \to \infty) ((1-x^2)/(x^3-x+1) )`

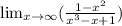
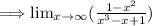
Step 1: Divide everything by the highest power in the denominator, x^3.

`\Longrightarrow \lim_(x \to \infty) (((1)/(x^3) -(x^2)/(x^3) )/((x^3)/(x^3) -(x)/(x^3) +(1)/(x^3) ) )`

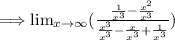
After simplifying we get,

`\Longrightarrow \lim_(x \to \infty) (((1)/(x^3) -(1)/(x) )/(1-(1)/(x^2) +(1)/(x^3) ) )`

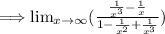
Step 2: Apply
`\lim_(x \to a) [(f(x))/(g(x)) ]=( \lim_(x \to a) f(x) )/( \lim_(x \to a) g(x) )`

`\Longrightarrow( \lim_(x \to \infty) ((1)/(x^3) -(1)/(x) ) )/( \lim_(x \to \infty) (1-(1)/(x^2) +(1)/(x^3)) )`

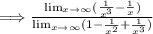
Step 3: Plug in "∞" and solve.

`\Longrightarrow( \lim_(x \to \infty) ((1)/((\infty)^3) -(1)/(\infty) ) )/( \lim_(x \to \infty) (1-(1)/((\infty)^2) +(1)/((\infty)^3)) )`

`\Longrightarrow( \lim_(x \to \infty) (0-0) )/( \lim_(x \to \infty) (1-0+0) )`

`\Longrightarrow \lim_(x \to \infty) ((0)/(1) ) = \boxed{0}`

`\Longrightarrow \boxed{\boxed{\lim_(x \to \infty) ((1-x^2)/(x^3-x+1) )=0}} \therefore Sol.`

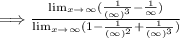
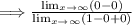
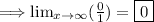
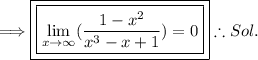
Thus, the limit is solved.