a.
 is
is
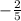
b. Moment Generating Function for Y is
![\[= (1)/(t+1) \cdot \infty \quad \text{(if t < -1)}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/40tw4kidq78f8ls5mt45wwg4507zhuj8fg.png)
c. V(Y) is
![\infty - 2^2 = \infty - 4 = \infty\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ruq6v2c98ydjnooumhttr16fkxn5c1p8z9.png)
a. Find
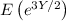 :
:
The expectation of a function of a random variable can be found using the formula:
![\[E(g(Y)) = \int_(-\infty)^(\infty) g(y) f_Y(y) \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/phgc56665ujskjng9giatda3g5kxexlaoa.png)
In this case,
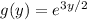 and
and
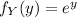 for
for
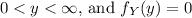 elsewhere.
elsewhere.
So,
![\[E\left(e^(3Y/2)\right) = \int_(0)^(\infty) e^(3y/2) \cdot e^y \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/h3zwmwb1ssk3mu6yrxdpddviwv9augvuuq.png)
![\[= \int_(0)^(\infty) e^((3y/2 + y)) \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/f6vlrag4cxtqc29erbsch1ifg4qwd4s6om.png)
![\[= \int_(0)^(\infty) e^((5y/2)) \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gm0nbzybzl4eh9kyp7bkdumowmheglgxx0.png)
Now, applying the integral, we get:
![\[E\left(e^(3Y/2)\right) = \left[(2)/(5) e^((5y/2))\right]_0^\infty\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/es9iy4tmroyl72ucb5huog1tsb7o6wpr6d.png)
![\[= (2)/(5) \left(e^((5 \cdot \infty / 2)) - e^((5 \cdot 0 / 2))\right)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rj4tilkxd1jaygwjkynl9boxkatjcktzbr.png)
![\[= (2)/(5) \left(0 - 1\right)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9qrvooqb9jr9un5ksybhiqiq54b668zpgt.png)
![\[= -(2)/(5)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/rd3xapix4ed9fve4gbhn5kdz82ahorvr9l.png)
b. Find the Moment Generating Function for Y.
The moment generating function (MGF) for a random variable Y is defined as:
![\[M_Y(t) = E(e^(tY))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/o3ln9opt2zguybddq5tqivivpb23rxgmbz.png)
So, in this case:
![\[M_Y(t) = E(e^(tY)) = \int_(0)^(\infty) e^(ty) \cdot e^y \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ezyaeern3e4lcq81ag5kucd4jnmd65n2sw.png)
![\[= \int_(0)^(\infty) e^((t+1)y) \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/th25yts6kk54umgbh5s0j8cdzwlda24un5.png)
Now, solving the integral:
![\[M_Y(t) = \left[(1)/(t+1) e^((t+1)y)\right]_0^\infty\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/f4b4yn0oysdoj8eswhxyfvkzl5o7vnucgf.png)
![\[= (1)/(t+1) \left(e^((t+1) \cdot \infty) - e^((t+1) \cdot 0)\right)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/z1n80ypnig1dg1txklhoatfu87zfkezej4.png)
![\[= (1)/(t+1) \left(\infty - 1\right)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qzp8n5rmlcrf7mzd2440xg57kpgsv0truz.png)
![\[= (1)/(t+1) \cdot \infty \quad \text{(if t < -1)}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/40tw4kidq78f8ls5mt45wwg4507zhuj8fg.png)
c. Find
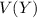 .
.
The variance of a random variable Y is given by:
![\[V(Y) = E(Y^2) - [E(Y)]^2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/eudnggcmazzqavf93h8ya8wo97ylpamyoa.png)
To find
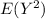 :
:
![\[E(Y^2) = \int_(0)^(\infty) y^2 \cdot e^y \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jkj44ostnccwo73ibx4pzjzt2usuz69tl9.png)
![\[= \int_(0)^(\infty) y^2 \cdot e^y \, dy\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/j4rae62nzv5pstkeqxxm60n26brsjnwduo.png)
Using integration by parts:
![\[E(Y^2) = \left[y^2 \cdot e^y - \int 2y \cdot e^y \, dy\right]_0^\infty\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/e0ckhhgsny942eefx5429ssp8ifjs87hlh.png)
![\[= \left[y^2 \cdot e^y - 2\left(y \cdot e^y - \int e^y \, dy\right)\right]_0^\infty\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/a15dq8oqmfl45546mr00lnw31260a9dpka.png)
![\[= \left[y^2 \cdot e^y - 2y \cdot e^y + 2e^y\right]_0^\infty\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7i0dg9i8ptv2uo9va05dblpyk7zp3pcy6v.png)
![\[= \lim_(y \to \infty) (y^2 e^y - 2y e^y + 2e^y) - (0^2 e^0 - 2 \cdot 0 \cdot e^0 + 2e^0)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1z66o7i4q9zq7n4aamuu5g9v3tg8ihj2ie.png)
![\[= \infty - 0 = \infty\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tm5hsmrvp0i7ilmuou821fcipvr61dqke9.png)
Since
 (previously calculated), now we can find
(previously calculated), now we can find
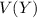 :
:
![\[V(Y) = E(Y^2) - [E(Y)]^2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/eudnggcmazzqavf93h8ya8wo97ylpamyoa.png)
![\[V(Y) = \infty - 2^2 = \infty - 4 = \infty\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ktltokltds2ka20v4iy7r84tskw53ogg7x.png)
The variance of Y is infinite, indicating high variability or dispersion of Y around its mean.
The complete question is here:
A random variable Y has the Density Function
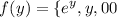 , elsewhere
, elsewhere
a. Find
 .
.
b. Find the Moment Generating Function for Y.
c. Find the
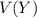 .
.