Question

I NEED HELP ON THIS FAST

Answer 1

`a. \quad \frac{\boxed{1}}{\boxed{3}}} \cdot \frac{\boxed{1}}{\boxed{2}}} = \frac{\boxed{1}}{\boxed{6}}}\\\\\\\\b. \quad \frac{\boxed{1}}{\boxed{3}}} \cdot \frac{\boxed{1}}{\boxed{3}}} = \frac{\boxed{1}}{\boxed{9}}}\\\\\\\\c. \quad \frac{\boxed{21}}{\boxed{26}}} \cdot \frac{\boxed{5}}{\boxed{26}}} = \frac{\boxed{105}}{\boxed{676}}}\\`

Explanation:

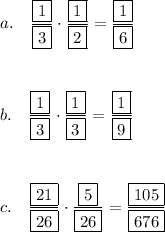
a.

When rolling a die(number cube) the sample space which is the set of all possible outcomes is {1, 2, 3, 4, 5, 6}

The probability of getting any single number on the face is the same = 1/6

For the first cube
P(3) = 1/6 and P(4) = 1/6
P(3 or 4) = P(3) + P(4) = 1/6 + 1/6 = 2/6 = 1/3

For the second cube
P(odd) = P(1 or 3 or 5) = P(1) + P(3) + P(5) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2

So the combined probability that the first cube shows 3 or 4 and the second an odd is given by
1/3 · 1/2 = 1/6

b.
There are three coins a penny, dime and quarter

Probability of selecting a penny = number of pennies/total number of coins = 1/3

Since we are replacing the selected coin for the second draw, the probability of selecting a penny is just the same as before = 1/3

P(selecting 2 pennies with replacement) = 1/3 · 1/3 = 1/9

c.

There are a total of 26 letters in the alphabet
There are 5 vowels in the alphabet: A, E, I, O, U

Therefore there are 26 - 5 = 21 consonants

P(drawing a consonant) = 21/26

P(drawing a vowel) = 5/26

Since we are replacing the first drawn letter, these probabilities do not change with successive draws.

Therefore
P(consonant first draw and vowel second draw)

= P(consonant) · P(vowel)

= 21/26 · 5/26

=105/676