Given that a mass,
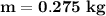 , swings in a circular path due to an attached string with a length,
, swings in a circular path due to an attached string with a length,
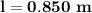 . Refer to IMAGE #1 for a picture of the situation.
. Refer to IMAGE #1 for a picture of the situation.
We are asked to answer the following...
(a) What forces always act on the mass throughout its swing?
(b) Draw force diagrams or free-body diagrams showing what forces are acting on the mass at the bottom of its swing vs the top.
(c) Given a velocity,
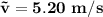 , when the mass is at the top of its swing, find the tension in the string,
, when the mass is at the top of its swing, find the tension in the string,
 .
.
(d) Given the maximum tension,
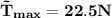 , what is the fastest the mass can travel at the bottom of its swing,
, what is the fastest the mass can travel at the bottom of its swing,
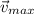 ?
?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
For part (a):
To answer part a lets list of all forces that can act on an object and then narrow them down.
List of forces:
1. Weight or the force of gravity which is the mass of an object multiplied by the magnitude of the acceleration from gravity
(
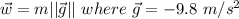 ).
).
2. Tension force which can be descried as a pulling force.
3. Normal force which is the force an object applies to prevent an object from traveling through its surface.
4. Friction force is a force that resists an objects motion.
5. Spring force is a force provided by a spring.
6. Air resistance force which is caused by air, can be interpreted as a friction force.
7. Electrical force is a force provided by charges.
8. Magnetic force which is a force provided by a magnetic field.
9. Buoyant force which is an upward force a fluid exherts on an object, can be interpreted as a normal force.
Right away we can eliminate 5,7,8, and 9. As we are not dealing with any springs, electricity, magnets, or fluids. We are also going to assuming there is no resistive forces acting on the ball so we can eliminate 4 and 6. The mass is not sitting on something so we can eliminate 3.
That leaves us with the gravitational force (weight) and the tension force. Which logically would make sense, gravity would act on the mass at all points in its path and the string will always provide a pulling force keeping the mass from unhooking and flying away in a straight line.
For part (b):
Refer to IMAGE #2
For part (c):
Refer to IMAGE #3
Add up forces acting in the centripetal axis. Note that the centripetal axis acts like the y axis and the tangential axis acts like the x axis.
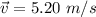
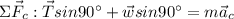 where
where
 is centripetal acceleration.
is centripetal acceleration.
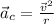
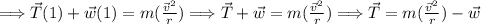
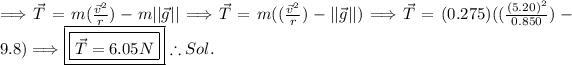
Thus, the tension in the string is found.
For part (d):
Refer to IMAGE #4
Add up forces acting in the centripetal axis. Note that the centripetal axis acts like the y axis and the tangential axis acts like the x axis.
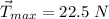
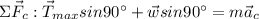
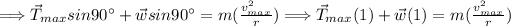
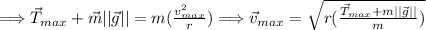
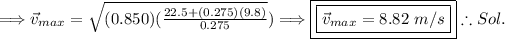
Thus, the max speed is found.