Question

37) Given A ABC determine the coordinates of A A'B'C' after a translation up 1 unit and left 2 units, followed by a

dilation with center at the origin and scale factor 0.5.
A. A'(-2,1), B'(0, -2), and C'(1,2)
B. A'(-2,2), B'(0, -4), and C'(1,4)
C. A'(-4,2), B'(0,6), and C' (2,4)
D. A'(-8,4), B'(0, 12), and C'(4, -8)ip

Answer 1

The answer is C given the information to the question above

Answer 2

A. A'(-2, 1), B'(0, -2), and C'(1, 2)

Explanation:

From inspection of the given diagram, the coordinates of the vertices of triangle ABC are:

• A = (-2, 1)
• B = (2, -5)
• C = (4, 3)

If the figure is translated left 2 units and up 1 unit, then the mapping rule of the translation is:

• 
  `(x, y) \;\rightarrow \;(x-2, y+1)`

If a figure is dilated by scale factor k with the origin as the center of dilation, the mapping rule is:

• 
  `(x, y)\; \rightarrow \;(kx, ky)`

Therefore, given the scale factor is 0.5, the final mapping rule that translates and dilates triangle ABC is:

• 
  `(x, y)\; \rightarrow \; \left(0.5(x-2), 0.5(y+1) \right)`

To find the coordinates of the vertices of triangle A'B'C', substitute the coordinates of the vertices of triangle ABC into the final mapping rule:

`\begin{aligned}A' &= (0.5(-2-2), 0.5(1+1)) \\&= (0.5(-4), 0.5(2)) \\&= (-2, 1)\end{aligned}`

`\begin{aligned}B' &= (0.5(2-2), 0.5(-5+1)) \\&= (0.5(0), 0.5(-4)) \\&= (0, -2)\end{aligned}`

`\begin{aligned}C' &=(0.5(4-2),0.5(3+1))\\&=(0.5(2),0.5(4))\\&=(1,2)\end{aligned}`

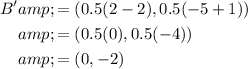
Therefore, the coordinates of the vertices of triangle A'B'C' are:

• A'(-2, 1), B'(0, -2), and C'(1, 2)