Question

Bryce, a mouse lover, keeps his four pet mice in a roomy cage, where they spend much of their spare time, when they're not sleeping or eating, joyfully scampering about on the cage's floor. Bryce tracks his mice's health diligently and just now recorded their masses as 0.02130.0213 kg, 0.01650.0165 kg, 0.01850.0185 kg, and 0.01930.0193 kg. At this very instant, the x‑x‑ and y‑y‑ components of the mice's velocities are, respectively, (0.675 m/s,−0.417 m/s)(0.675 m/s,−0.417 m/s) , (−0.249 m/s,−0.809 m/s)(−0.249 m/s,−0.809 m/s) , (0.395 m/s,0.953 m/s)(0.395 m/s,0.953 m/s) , and (−0.207 m/s,0.227 m/s)(−0.207 m/s,0.227 m/s) . Calculate the x‑x‑ and y‑y‑ components of Bryce's mice's total momentum, pxpx and pypy .

Answer 1

Answer:
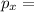`p_(x)=` 0.0135814 kg.m/s

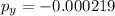`p_(y)=-0.000219` kg.m/s

Step-by-step explanation: When an object with mass is in motion, we say the object has momentum (p). Momentum is dependent on mass and velocity:

p = m.v

The total momentum of Bryce's mice is calculated as

x-axis

`p_(x)=\Sigma m.v_(x)`

`p_(x)=[(0.0213)(0.675)+(0.0165)(-0.249)+(0.0185)(0.395)+(0.0193)(-0.207)]`

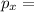`p_(x)=` 0.0135814

At the x-axis, total momentum of Bryce's mice is 0.0135814 kg.m/s.

y-axis

`p_(y)=\Sigma m.v_(y)`

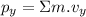
`p_(y)=[(0.0213)(-0.417)+(0.0165)(-0.809)+(0.0185)(0.953)+(0.0193)(0.227)]`

`p_(y)=-0.000219`

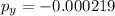
At the y-axis, total momentum of Bryce's mice is -0.000219 kg.m/s.