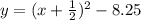Answer:
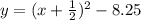
Explanation:
First, we move the c in
 to the other side of the equation by adding 8 onto both sides:
to the other side of the equation by adding 8 onto both sides:
 .
.
Then, since
 has no coefficient, we make the left side a perfect square trinomial by adding
has no coefficient, we make the left side a perfect square trinomial by adding
 on both sides of the equation. We do this because adding this to the equation will make the left side equal to
on both sides of the equation. We do this because adding this to the equation will make the left side equal to
 (plus-minus because the sign depends on if b is negative or positive):
(plus-minus because the sign depends on if b is negative or positive):
 .
.
Then, simplify the left side:
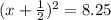
Finally, subtract 8.25 on both sides to make it vertex form: