Question

Find the average force the cylinder exerts on the nail while pushing it into the block. Ignore the effects of the air. Express your answer with the appropriate units. A nail is partially inserted into a block of wood, with a length of 0.0300 m protruding above the top of the block. To hammer the nail in the rest of the way, you drop a 20.0 kg metal cylinder onto it. The cylinder rides on vertical tracks that exert an upward friction force of 16.0 N on the cylinder as it falls. You release the cylinder from rest at a height of 1.50 m above the top of the nail. The cylinder comes to rest on top of the block of wood, with the nail fully inside the block. Use the work-energy theorem to find the speed of the cylinder just as it hits the nail

Express your answer with the appropriate units.

Answer 1

1. The speed of the cylinder just as it hits the nail is approximately
`\(5.20\, \text{m/s}\)`.

2. The negative sign indicates that the force is acting in the opposite direction of motion, which is expected as it opposes the cylinder's motion. So, the average force the cylinder exerts on the nail while pushing it into the block is approximately 180.14 Newtons (N).

To find the speed of the cylinder just as it hits the nail using the work-energy theorem, we can consider the initial potential energy of the cylinder at the height it's released and its final kinetic energy when it hits the nail. According to the work-energy theorem:

The work done on an object

`\[W_{\text{net}} = \Delta KE\]`

Where:

• 
  `\(W_{\text{net}}\)` is the net work done on the system (cylinder and nail).
• 
  `\(\Delta KE\)` is the change in kinetic energy.

First, let's calculate the initial potential energy of the cylinder:

`\[PE_{\text{initial}} = mgh\]`

Where:

• 
  `\(m\)` is the mass of the cylinder (20.0 kg).
• 
  `\(g\)` is the acceleration due to gravity (approximately 9.81 m/s²).
• 
  `\(h\)` is the height from which the cylinder is released (1.50 m above the top of the nail).

`\[PE_{\text{initial}} = (20.0\, \text{kg})(9.81\, \text{m/s}^2)(1.50\, \text{m})\]`

`\[PE_{\text{initial}} = 294.3\, \text{Joules}\]`

Now, let's calculate the final kinetic energy of the cylinder when it hits the nail.

`\[KE_{\text{final}} = (1)/(2)mv^2\]`

Where:

• 
  `\(m\)` is the mass of the cylinder (20.0 kg).
• 
  `\(v\)` is the speed of the cylinder just as it hits the nail (what we want to find).

Now, we can apply the work-energy theorem:

`\[W_{\text{net}} = \Delta KE\]`

Since the cylinder experiences an upward friction force of 16.0 N, the net work done on the system is negative (the friction force opposes the motion):

`\[W_{\text{net}} = -F_{\text{friction}} \cdot d\]`

Where:

• 
  `\(F_{\text{friction}}\)` is the friction force (16.0 N).
• 
  `\(d\)` is the distance the cylinder travels (1.50 m).

`\[W_{\text{net}} = -(16.0\, \text{N})(1.50\, \text{m})\]`

`\[W_{\text{net}} = -24.0\, \text{Joules}\]`

Now, we can use the work-energy theorem to find the speed \(v\) of the cylinder:

`\[-24.0\, \text{J} = \Delta KE = KE_{\text{final}} - PE_{\text{initial}}\]`

Substitute the values:

`\[-24.0\, \text{J} = \left((1)/(2)(20.0\, \text{kg})v^2\right) - 294.3\, \text{J}\]`

Now, isolate v:

`\[(1)/(2)(20.0\, \text{kg})v^2 = -24.0\, \text{J} + 294.3\, \text{J}\]`

`\[(1)/(2)(20.0\, \text{kg})v^2 = 270.3\, \text{J}\]`

Now, solve for v:

`\[v^2 = \frac{2 \cdot 270.3\, \text{J}}{20.0\, \text{kg}}\]`

`\[v^2 = 27.03\, \text{m}^2/\text{s}^2\]`

Take the square root:

`\[v = \sqrt{27.03\, \text{m}^2/\text{s}^2} \approx 5.20\, \text{m/s}\]`

So, the answer is approximately
`\(5.20\, \text{m/s}\)`.

Now, we can use the impulse-momentum theorem to find the average force
`( $\left.F_{\text {avg }}\right)$` exerted by the cylinder on the nail:

`$$F_{\text {avg }} \cdot \Delta t=\Delta p$$`

We can rearrange the equation to solve for t:

`$$\begin{aligned}& 0 \mathrm{~m} / \mathrm{s}=5.20 \mathrm{~m} / \mathrm{s}+a t \\& a t=-5.20 \mathrm{~m} / \mathrm{s}\end{aligned}$$`

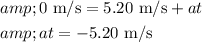
Now, let's find a.

`$$a=\frac{F_{\text {gravity }}-F_{\text {friction }}}{m}$$`

`$$\begin{aligned}& a=\frac{(20.0 \mathrm{~kg})\left(9.81 \mathrm{~m} / \mathrm{s}^2\right)-16.0 \mathrm{~N}}{20.0 \mathrm{~kg}} \\& a=\frac{196.2 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}^2-16.0 \mathrm{~N}}{20.0 \mathrm{~kg}} \\& a=\frac{196.2 \mathrm{~N}-16.0 \mathrm{~N}}{20.0 \mathrm{~kg}} \\& a=\frac{180.2 \mathrm{~N}}{20.0 \mathrm{~kg}} \\& a=9.01 \mathrm{~m} / \mathrm{s}^2\end{aligned}$$`

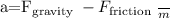
Now that we have the acceleration
`$(a)$`, we can find the time
`$(t)$` it takes for the cylinder to come to rest using the kinematic equation:

`$$\begin{aligned}& a t=-5.20 \mathrm{~m} / \mathrm{s} \\& \left(9.01 \mathrm{~m} / \mathrm{s}^2\right) t=-5.20 \mathrm{~m} / \mathrm{s} \\& t=\frac{-5.20 \mathrm{~m} / \mathrm{s}}{9.01 \mathrm{~m} / \mathrm{s}^2} \\& t \approx-0.577 \mathrm{~s}\end{aligned}$$`

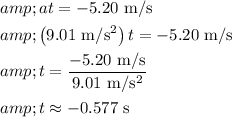
Now that we have the time
`$(t)$`, we can calculate the average force
`$\left(F_{\text {avg }}\right)$` :

`$$\begin{aligned}& F_{\text {avg }} \cdot(-0.577 \mathrm{~s})=104.0 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s} \\& F_{\text {avg }}=\frac{104.0 \mathrm{~kg} \cdot \mathrm{m} / \mathrm{s}}{-0.577 \mathrm{~s}} \\& F_{\text {avg }} \approx-180.14 \mathrm{~N}\end{aligned}$$`

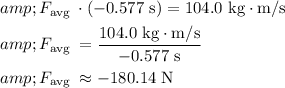
The answer is -180.14 N.

The complete question is here:

Answer 2

The speed of the cylinder just as it hits the nail is determined as 5.2 m/s.

How to calculate the speed of the cylinder?

The speed of the cylinder is calculated by applying work energy theorem as follows;

K.E of cylinder = P.E at top - work done by friction

¹/₂mv² = mgh - Fd

where;

• m is the mass of the metal cylinder
• g is gravity
• h is the height of fall
• d is the distance in which the friction acts on the hammer

¹/₂mv² = mgh - Fd

¹/₂(20)v² = (20 x 9.8 x 1.5) - (16 x (1.5 - 0.03)

10v² = 270.48

v² = 27.048

v = √ (27.048)

v = 5.2 m/s

Thus, the speed of the cylinder just as it hits the nail is determined as 5.2 m/s.