Question

consider the line (2,3,-7) t(-1,-2,1). find the smallest possible distance from the line to the origin.

Answer 1

Explanation:

finding the smallest possible distance from the line to the origin follows as

the normal vector=(-1,-2,1)

using direction vector we need to create the equation of the plane

-1(x-2)-2(y-3)+1(z+7)=0

we get;

-x+2-2y+6+z+7=0

-x-2y+z+13=0

x=2-t; y=2-3t; z=-7+t

on substituting;

-1(2-t)-2(3-2t)+1(-7+t)+13=0

-2+t-6+4t-7+t+13=0

we get;

t=1

so point is(1,1,-6)

distance from point to origin

d=
`√((1^2+1^2+(-6)^2))`=
`√(38)`

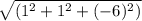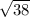
therefore

the answer is
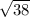`√(38)`=6.16