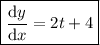Question

Math hw for tonight
help solve this problem! Thank you!
ap cal bc

Answer 1

2t + 4

Explanation:

A parametric equation is one where x and y are defined separately in terms of a third variable (often the parameter t).

To find dy/dx from parametric equations, differentiate each equation with respect to the parameter t, then use the chain rule:

`\boxed{\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}t} * \frac{\text{d}t}{\text{d}x}}`

Differentiate the two parametric equations with respect to t:

`x=t-3 \implies \frac{\text{d}x}{\text{d}t}=1`

`y=t^2+4t \implies \frac{\text{d}y}{\text{d}t}=2t+4`

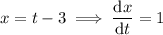
Use the chain rule to combine them:

`\begin{aligned}\implies \frac{\text{d}y}{\text{d}x}&=\frac{\text{d}y}{\text{d}t} * \frac{\text{d}t}{\text{d}x}\\\\&=(2t+4) * (1)/(1)\\\\&=2t+4\end{aligned}`

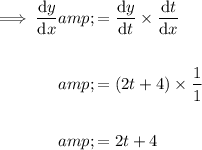
Therefore:

`\boxed{\frac{\text{d}y}{\text{d}x}=2t+4}`

Answer 2

first option

Explanation:

differentiate using the power rule

`(d)/(dx)` (a
`x^(n)` ) = na
`x^(n-1)`

then

`(dy)/(dx)` =
`(dy)/(dt)` ×
`(dt)/(dx)` =
`((dy)/(dt) )/((dx)/(dt) )`

y = t² + 4t

`(dy)/(dt)` = 2t + 4

x = t - 3

`(dx)/(dt)` = 1

then

`(dy)/(dx)` =
`(2t+4)/(1)` = 2t + 4