Answer:

Third answer option
Explanation:
We are given the polar equation as
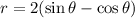
and asked to convert it into rectangular form
We have the following equations which relate (r, θ) in polar form to (x, y) in rectangular form
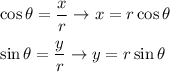
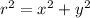
Original polar equation:
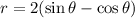
Expand the right side:
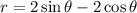
Substitute for sinθ and cosθ in terms of x and y
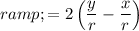
Multiply both sides by r:
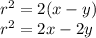
Substitute
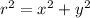 on the left side:
on the left side:
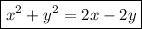
This would be the third answer opton