Answer:
260
Explanation:
The z score for a normal distribution is given by the formula
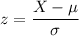
where
X is the data point, μ is the mean and σ is the standard deviation
Given
Mean μ = 500
Standard deviation σ = 80
z-score = -3
and plugging in these values for z-score formula we get
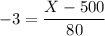
==>
-240 = X - 500
-240 + 500 = X
260 = X
or
X = 260