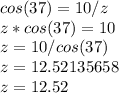Question

What is the value of z in the triangle?

Enter your answer in the box. Round your final answer to the nearest hundredth.

Answer 1

z = 12.52 in.

Explanation:

Because this is a right triangle, we can solve for z using on the trigonometric ratios.

If we allow 37° to be our reference angle, the 10 in. side is the adjacent side and z (directly across from the right angle) is the hypotenuse.

Thus, we can use the cosine ratio which is

`cos(angle)=(adjacent)/(hypotenuse)`

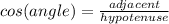
Now, we can plug everything into the formula and solve for z, the hypotenuse:

`cos(37)=10/z\\z*cos(37)=10\\z=10/cos(37)\\z=12.52135658\\z=12.52`