Question

Solve sin²(x - 1) - 2 sin(x - 1) = 3 over [0, 2π)

Answer 1

`x=(3\pi )/(2) +1`

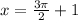
Explanation:

Subtract 3 from both sides of the equation.

`sin^2(x-1)-2sin(x-1)-3=0`

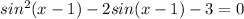
Factor using the AC method.

Consider the form
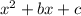`x^2+bx+c` . Find a pair of integers whose product is
`c` and whose sum is
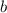`b` . In this case, whose product is −3 and whose sum is −2

We get −3 and 1.

Write the factored form using these integers.

`(sin(x-1)-3)(sin(x-1)+1)=0`

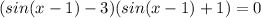
If any individual factor on the left side of the equation is equal to 0, the entire expression will be equal to 0.

`sin(x-1)-3=0`

`sin(x-1)+1=0`

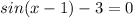
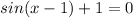
Solve for x in each equation.

`sin(x-1)-3=0`

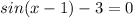
Add 3 to both sides of the equation.

`sin(x-1)=3`

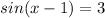
The range of sine is
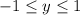`-1\leq y\leq 1` . Since 3 does not fall in this range, there is no solution. No solution

Solve for x.

`sin(x-1)+1=0`

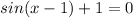
Subtract 1 from both sides of the equation.

`sin(x-1)=-1`

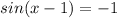
Take the inverse sine of both sides of the equation to extract
`x` from inside the sine.

`x-1=arcsin(-1)`

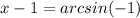
The exact value of
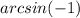`arcsin(-1)` is
`-(\pi )/(2)`

`x-1=-(\pi )/(2)`

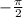
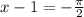
Add 1 to both sides of the equation.

`x=-(\pi )/(2)+1`

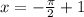
The sine function is negative in the third and fourth quadrants. To find the second solution, subtract the solution from
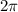`2\pi` , to find a reference angle. Next, add this reference angle to
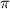`\pi` to find the solution in the third quadrant.

`x-1=2\pi +(\pi )/(2) +\pi -2\pi`

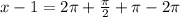
Subtract
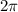`2\pi` from
`2\pi +(\pi )/(2) +\pi -2\pi`

The resulting angle of
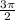`(3\pi )/(2)` is positive, less than
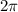`2\pi`, and coterminal with
`2\pi +(\pi )/(2) +\pi`.

`x-1=(3\pi )/(2)`

`x=(3\pi )/(2)+1`

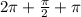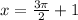
Find the period of
`sin(x+1)`.

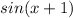The period of the function can be calculated using
`(2\pi )/(|B|)`.

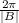Replace
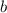`b` with 1 in the formula for period.

`(2\pi )/(|1|)=(2\pi )/(1)=2\pi`

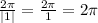
Add
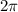`2\pi` to every negative angle to get positive angles.

Add
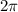`2\pi` to
`-(\pi )/(2)+1` to find the positive angle.

`-(\pi )/(2)+1+2\pi`

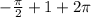
After some algebra we get
`x=(3\pi )/(2) +1`

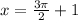
The period of the
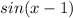`sin(x-1)` function is
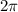`2\pi` so values will repeat every
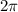`2\pi`radians in both directions.

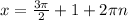`x=(3\pi )/(2) +1+2\pi n` for any integer
`n`.

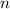The final solution is all the values that make
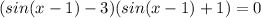`(sin(x-1)-3)(sin(x-1)+1)=0` true.