Question

Given the equation f(x)=-x^2-2x+3 what is the equation of the axis of symmetry?

Answer 1

x = -1

Explanation:

Pre-Solving

We are given the following function: f(x) = -x²-2x+3

We want to find the equation of the axis of symmetry.

The axis of symmetry is a line that we can draw down the center of a parabola. It will split the parabola into two equal halves.

The axis of symmetry is given with the equation x = h, where h is the value of the vertex.

The vertex is either the highest or lowest point on the parabola, so it makes sense that the x value of it will split the parabola into two equal halves.

Solving

We need to find the value of x at the vertex.

It can be found with the equation
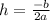`h = (-b)/(2a)`, where b is the coefficient of x in the equation and a is the coefficient of x² in the equation.

We can see that because there is a - sign in front of x², the coefficient of x² is -1. We can also see that there is a -2 in front of x, which means that the coefficient in front of x is -2.

Let's substitute these values in.

`h = (-b)/(2a)`

`h = (--2)/(2(-1))`

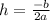
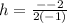
Simplify

`h = (+2)/(-2)`

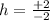
h = -1

So, the value of x at the vertex is -1.

Therefore, the axis of symmetry is x = -1.