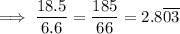Question

Given the four rational numbers below, come up with the greatest sum, difference, product, and quotient, using two of the numbers for each operation. Numbers may be used more than once. Show your work.​

Answer 1

`\textsf{Greatest sum}=25.1=25(1)/(10)`

`\textsf{Greatest difference}=30.9=30(9)/(10)`

`\textsf{Greatest product}=122.1=122(1)/(10)`

`\textsf{Greatest quotient}=2.8\overline{03}=2(53)/(66)`

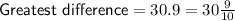
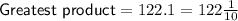
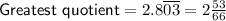
Explanation:

Method 1

First, rewrite each number as an improper fraction with the common denominator of 10.

`6.6=(66)/(10)`

`-4(3)/(5)=-(4 \cdot 5+3)/(5)=-(23)/(5)=-(23 \cdot 2)/(5 \cdot 2)=-(46)/(10)`

`18(1)/(2)=(18 \cdot 2+1)/(2)=(37)/(2)=(37\cdot 5)/(2\cdot 5)=(185)/(10)`

`-12.4=-(124)/(10)`

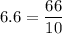
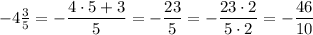
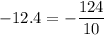
Now order the improper fractions from smallest to largest:

`-(124)/(10),\;\;-(46)/(10),\;\;(66)/(10),\;\;(185)/(10)`

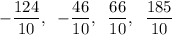
The greatest sum can be found by adding the largest two numbers:

`\implies (66)/(10)+(185)/(10)=(66+185)/(10)=(251)/(10)=25.1=25(1)/(10)`

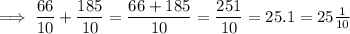
The greatest difference can be found by subtracting the smaller number from the largest number:

`\implies (185)/(10)-\left(-(124)/(10)\right)=(185+124)/(10)=(309)/(10)=30.9=30(9)/(10)`

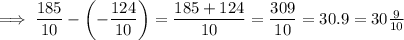
The greatest product can be found by multiplying the largest two numbers:

`\implies (66)/(10)\cdot (185)/(10)=(66\cdot 185)/(10 \cdot 10)=(12210)/(100)=122.1=122(1)/(10)`

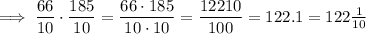
The greatest quotient can be found by dividing the largest number by the smallest number, given the two numbers have the same sign.

`\implies (185)/(10) / (66)/(10)= (185)/(10) \cdot (10)/(66)=(185)/(66)=2(53)/(66)`

`\hrulefill`

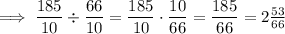
Method 2

Rewrite all the numbers as decimals:

`6.6`

`-4(3)/(5)=-4.6`

`18(1)/(2)=18.5`

`-12.4`

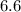
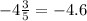
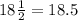
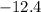
Now order the decimals from smallest to largest:

`-12.4, \;\; -4.6, \;\;6.6,\;\;18.5`

The greatest sum can be found by adding the largest two numbers:

`\begin{array}{rr}&6.6\\+&18.5\\\cline{2-2} &25.1\\ \cline{2-2}&^1^1\;\;\;\end{array}`

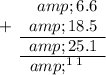
The greatest difference can be found by subtracting the smallest number from the largest number:

`18.5-(-12.4)=18.5+12.4`

`\begin{array}{rr}&18.5\\+&12.4\\\cline{2-2} &30.9\\ \cline{2-2}&^1\;\;\;\;\end{array}`

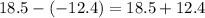
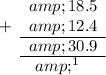
The greatest product can be found by multiplying the largest two numbers:

`\begin{array}{rr}&18.5\\*&6.6\\\cline{2-2} &11.10\\+&111.00\\ \cline{2-2}&122.10\end{array}`

The greatest quotient can be found by dividing the largest number by the smallest number, given the two numbers have the same sign.

`\implies (18.5)/(6.6)=(185)/(66)=2.8\overline{03}`