Answer:
Explanation:
Here A be n×n matrix with real enties
y= Ax=xA is vector space.
Let m be set of all n*n matrix with real enties then m is vector space over IR.
we show y is vector subspace of m.
Here
 identity matrix
identity matrix
IA=AI
∴ I ∈ y
∴ y is non empty subset of m.
Also if
 ,
,
 ∈ y ⇒ A
∈ y ⇒ A
 =
=
 A ,A
A ,A
 =
=
 A
A
for
 ∈ IR arbitrary
∈ IR arbitrary
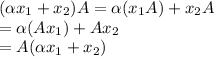
Hence
 ∈ y ∀
∈ y ∀
 ∈ y
∈ y
∴ y is subspace of m.
∴ y is vector space.