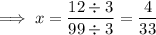Question

Express in the form of a rational number: 0.1212….​

Answer 1

`0.1212...=(4)/(33)`

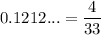
Explanation:

A repeating decimal is a decimal number with a digit (or group of digits) that repeats forever.

There are three ways to show a repeating decimal:

• Several duplicates of the repeating digit or block of digits, followed by an ellipsis, e.g. 0.3333... or 0.123123...
• A dot or a line above a repeated digit, e.g.
  `\sf 0.\.{3}` or
  `\sf 0.\overline{3}`
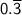
• A line above a repeating block of multiple digits, e.g.
  `\sf 0.\overline{123}`

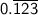
0.1212... is a repeating decimal as there are two duplicates of the repeating block of digits "12" followed by an ellipsis.

To express a repeating decimal as a rational number, begin by assigning the decimal to a variable:

`x=0.1212...=0.\overline{12}`

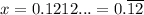
Multiply both sides by 100:

`\implies x \cdot 100=0.\overline{12}\cdot 100`

`\implies 100x=12.\overline{12}`

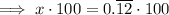
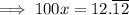
Subtract the first equation from the second to eliminate the part after the decimal:

`\begin{array}{crcr}& 100x & = & 12.\overline{12}\\- & x & = & 0.\overline{12}\\\cline{2-4} & 99x & = & 12\phantom{.12}\\\end{array}`

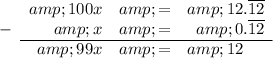
Divide both sides of the equation by 99:

`\implies (99x)/(99)=(12)/(99)`

`\implies x=(12)/(99)`

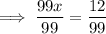
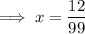
Reduce the fraction to is simplest form by dividing the numerator and denominator by 3:

`\implies x=(12 / 3)/(99 / 3)=(4)/(33)`

`\textsf{Therefore, $0.1212...$ expressed in the form of a rational number is\;$(4)/(33)$}.`