Question

The function f(x) = x^3 + 8x^2 + x – 42 has zeros located at –7, 2, –3. Verify the zeros of f(x) and explain how you verified them. Describe the end behavior of the function.

Answer 1

Given that the function:

`f(x)=x^3+8x^2+x-42`

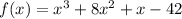
The function has zeros located at -7, 2, -3

First, let check f(2) = 0

`2^3+8(2)+2-42=0`

`8+16+2-42=0`

`42-42=0`

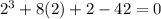
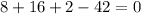
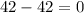
Therefore, f(2) has a zero, that is (x - 2) is a factor of the polynomial function..

So, divide the given function by (x-2) to get the quadratic function.

`(x^3+8x^2+x-42)/(x-2) =x^2+10x+21`

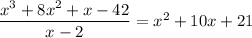
Now, solve the quadratic function.

`x^2+10x+21=0`

`x^2+7x+3x+21=0`

`x(x+7)+3(x+7)=0`

`x+7=0 \ \text{and} \ x+3=0`

`x=-7 \ \text{or} -3`

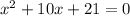
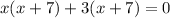
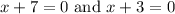
From the explanation above, it shows that -7, 2, and -3 are the roots (zeros) of the given polynomial function.

Thus, the behavior of the function can be described by using the degree and the leading coefficient.

The leading degree is 3 and the leading coefficient is 1.

So since the leading degree is odd (3), the end of the function will point in the opposite direction.

And since the leading coefficient is positive (+1), the graph rises to the right.

Hence, the behavior of the function falls to the left and rises to the right.