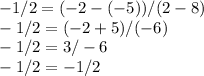Question

Find the value of

n​ so that the line that goes through the points

(8,n)​ and

(2,−2)​ is perpendicular to

y=2x+4​​.

Answer 1

n = -5

Explanation:

We know that when two lines are perpendicular, the slopes of the two lines are negative reciprocals as

`m_(2)=-(1)/(m_(1) )`, where m2 is the slope of the line we're usually not given, and m1 is the slope of the line we're given

Thus, we know that m2 must equal -1/2 from the formula since m1 is 2:

`m_(2)=-(1)/(2)`

Of course, -1/2 is already simplified so m2 is the slope of the line passing through (8, n) and (2, -2)

To find n, we must use our knowledge of the slope formula that gives us the slope, m:

`m=(y_(2)-y_(1) )/(x_(2)-x_(1) )`, where x1 and y1 are one point on the line and x2 and y2 are another point on the line:

If we allow (8, n) to be our x1 and y1 point and allow (2, -2) to be our x1 and y2 point and -1/2 to be our m, we can now solve for m by plugging everything into the slope formula and solving for n (aka y1 in the formula:

`-1/2=(-2-n)/(2-8)\\ \\-1/2=(-2-n)/(-6)\\ \\3=-2-n\\\\5=-n\\\\-5=n`

We can even check that we get -1/2 when we plug in -5 into the slope formula:

`-1/2=(-2-(-5))/(2-8)\\-1/2=(-2+5)/(-6)\\-1/2=3/-6\\-1/2=-1/2`