Answer:
6.03
Explanation:
In math terms, we can model the area left when cutting a circle out of a triangle as subtracting the area of a circle inscribed in a triangle.
There was only one side length of the triangle given (its base), so we can assume that it is an isosceles triangle with the given height.
To find the radius of the triangle, we can use the formula:
r = (A / s)
where r is the radius of the inscribed circle, A is the area of the triangle, and s is the semiperimeter (half-perimeter) of the triangle.
Finding the area of the triangle:
A = (1/2) * b * h
A = (1/2) * 6 * 5
A = 15
Finding the length of the congruent sides of the triangle:

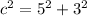
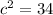
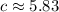
Finding the semiperimeter:
s = (side1 + side2 + side3) / 2
s = (5.83 + 5.83 + 6) / 2
s ≈ 8.83
Plugging these values into the radius formula:
r = A / s
r = 15 / 8.83
r ≈ 1.69
From here, we can get the area of the circle cutout:
A(circle) = πr²
A(circle) = π(1.69)²
A(circle) ≈ 8.97
Finally, we can get the leftover area by subtracting the area of the circle from the area of the triangle:
A = A(triangle) - A(circle)
A = 15 - 8.97
A = 6.03