Question

Identical balls are dropped from the same initial height and bounce back to half the initial height. In Case 1, the ball bounces off a cement floor, and in Case 2, the ball bounces off a piece of stretchy rubber. Two cases of a ball dropping and bouncing off of a surface. In case one, the ball approaches a cement floor, comes in contact, momentarily comes to rest, and then bounces off with a velocity smaller than the approach velocity. In case 2, the ball approaches a piece of stretchy rubber. When the ball comes in contact with the rubber, it deforms the rubber and comes momentarily to rest. The ball bounces off again with a velocity smaller than the approach velocity, and the rubber regains its original shape. In both cases, the balls are dropped from the same initial height and reach the same final height. In which case is the magnitude of the ball's change in momentum the greatest

Answer 1

the impulse must be the same in these two cases F t = m (
`√(2g h_f ) - √(2g h_o)`)

Step-by-step explanation:

For this exercise we use the relationship between momentum and momentum

I = Δp

F t = m v_f - m v₀

To know the speed we use the conservation of energy

starting point. Highest point

Em₀ = U = m g h

fincla point. Just before the crash

Em_f = K = ½ m v²

energy is conserved

Em₀ = Em_f

m g h = ½ m v²

v =
`√(2gh)`

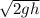
we substitute in the impulse relation

F t = m (
`√(2g h_f ) - √(2g h_o)`)

therefore we can see that as in case the initial and final heights are equal, the impulse must be the same in these two cases