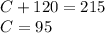Question

Janie is selling tickets for a high school play. Child tickets cost $3 and adult tickets cost $14.

She sells 215 tickets and collects $1965.

Answer 1

A = 120; C = 95

Explanation:

We will need a system of equations to solve for C, the number of child tickets and A, the number of adult tickets.

We know that the sum of the revenue earned from both the child tickets and the adult tickets = the total revenue

• (price of child tickets * quantity of child tickets) + (price of adult tickets * quantity of adult tickets) = 1965

Thus, our first equation is 3C + 14A = 1965

We also know that the sum of the total number of child and adult tickets = the the total number of tickets

• total quantity of child tickets + total quantity of adult tickets = 215

Thus, our other equation is C + A = 215

We can solve using substitution by first isolating c in the second equation:

`C+A=215\\C=-A+215`

Now, we can plug in the equation we just made for C in the first equation in our system to solve for A:

`3(-A+215)+14A=1965\\-3A+645+14A=1965\\11A+645=1965\\11A=1320\\A=120`

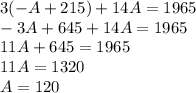
Finally, we can solve for C using the second equation in our system by plugging in 120 for A:

`C+120=215\\C=95`