Question

At a local Brownsville play production, 420 tickets were sold. The ticket prices varied on the seating arrangements and cost $8, $10, or $12. The total income from ticket sales reached $3920. If the combined number of $8 and $10 priced tickets sold was 5 times the number of $12 tickets sold, how many tickets of each type were sold?

Answer 1

Number of $ 8 priced tickets = 210

Number of $10 priced tickets = 140

Number of $ 12 priced tickets = 70

Explanation:

Framing and solving equations with three variables:

Let the number of $ 8 priced tickets = x

Let the number of $10 priced tickets = y

Let the number of $ 12 priced tickets = z

Total number of tickets = 420

x + y + z = 420 --------------(i)

Total income = $ 3920

8x + 10y + 12z = 3920 ----------------(ii)

Combined number of $8 and $10 priced tickets= 5 * the number of $12 priced tickets

x + y = 5z

x + y - 5z = 0 -------------------(iii)

(i) x + y + z = 420

(iii) x + y - 5z = 0

- - + + {Subtract (iii) from (i)}

6z = 420

z = 420÷ 6

`\sf \boxed{\bf z = 70}`

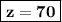
(ii) 8x + 10y + 12z = 3920

(iii)*8 8x + 8y - 40z = 0

- - + - {Now subtract}

2y + 52z = 3920 -----------------(iv)

Substitute z = 70 in the above equation and we will get the value of 'y',

2y + 52*70 = 3920

2y + 3640 = 3920

2y = 3920 - 3640

2y = 280

y = 280 ÷ 2

`\sf \boxed{\bf y = 140}`

substitute z = 70 & y = 140 in equation (i) and we can get the value of 'x',

x + 140 + 70 = 420

x + 210 = 420

x = 420 - 210

`\sf \boxed{x = 210}`

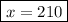
Number of $ 8 priced tickets = 210

Number of $10 priced tickets = 140

Number of $ 12 priced tickets = 70