Question

I'm checking over my new e-bike (electric assist bicycle). I prop it up so that the back wheel can spin freely (its not touching the ground). I give it a push and watch it spin. Then, at time t=0, when its angular velocity is 20.0 rad/s , I turn on the electric motor so that the wheel has a constant angular acceleration of 25.0 rad/s2 . Then at time t = 1.70 s I turn the motor off. From then on, the wheel turns through an angle of 438 rad as it gradually slows to a stop, at constant angular deceleration. Part A Through what total angle did the wheel turn between t=0 and the time it stopped? Express your answer in radians. Part B At what time does the wheel stop? Express your answer in seconds. Part C What was the wheel's angular acceleration as it slowed down? Express your answer in radians per second per second.

Answer 1

The total angle the wheel turned between t=0 and the time it stopped was 91.7 rad. The wheel stopped at a time of 0.8 s. The wheel's angular acceleration as it slowed down was -25.0 rad/s².

Step-by-step explanation:

Part A:

To find the total angle the wheel turned between t=0 and the time it stopped, we need to calculate the angle turned during the time the motor was on and the angle turned while slowing down. When the motor is on, the wheel experiences a constant angular acceleration of 25.0 rad/s². The time it was on is t = 1.70 s. Using the equation θ = ω₀t + 1/2αt² and substituting the values, we find θ = (20.0 rad/s)(1.70 s) + 1/2(25.0 rad/s²)(1.70 s)² = 91.7 rad.

When the motor is turned off, the wheel decelerates at a constant angular deceleration. The total angle turned during deceleration can be found using the equation ω = ω₀ + αt and rearranging the equation to find θ = ω₀t + 1/2αt². Rearranging again, we get the equation t = (ω - ω₀)/α and substituting the values, we find t = (0 - 20.0 rad/s)/(-25.0 rad/s²) = 0.8 s. The time it takes for the wheel to stop is 0.8 s.

Part C:

The wheel's angular acceleration as it slowed down can be found using the equation α = (ω - ω₀)/t and substituting the values, we get α = (0 - 20.0 rad/s)/0.8 s = -25.0 rad/s².

Answer 2

Part A:The wheel turned through a total angle of 595 rad between
`\(t=0\)`and the time it stopped.

Part B: The wheel stops at approximately
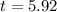`\(t = 5.92\)` s.

Part C: The wheel's angular acceleration as it slowed down was
`\(-25.0\)`rad/s².

Step-by-step explanation:

Part A:

To find the total angle turned
`(\(\theta\))` between
`\(t=0\)` and the time the motor is turned off
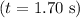`(\(t=1.70\) s)`, we use the kinematic equation for rotational motion:

`\[ \theta = \omega_i t + (1)/(2) \alpha t^2 \]`

where
`\(\omega_i\)` is the initial angular velocity,
`\(\alpha\)` is the angular acceleration, and
`\(t\)` is the time. Substituting the given values
`(\(\omega_i = 20.0\) rad/s`,
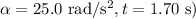`\(\alpha = 25.0\) rad/s^2, \(t = 1.70\) s)`, we get:

`\[ \theta = (20.0 \, \text{rad/s} * 1.70 \, \text{s}) + (1)/(2) * 25.0 \, \text{rad/s²} * (1.70 \, \text{s})^2 \]`

Solving this expression yields
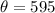`\(\theta = 595\)` rad.

Part B:

To determine when the wheel stops
`(\(t\)),` we use the kinematic equation for angular velocity:

`\[ \omega_f = \omega_i + \alpha t \]`

where
`\(\omega_f\)` is the final angular velocity. Rearranging for time, we get:

`\[ t = (\omega_f - \omega_i)/(\alpha) \]`

Substituting the given values
`(\(\omega_f = 0\) rad/s, \(\omega_i = 20.0\) rad/s, \(\alpha = -25.0\) rad/s^2),` we find:

`\[ t = (0 - 20.0)/(-25.0) \]`

Solving this expression gives
`\(t \approx 5.92\) s`.

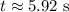Part C:

The angular acceleration as the wheel slows down
`(\(\alpha\))` is given as
`\(-25.0\)`rad/s². The negative sign indicates deceleration or a decrease in angular velocity over time. This value represents the constant angular acceleration experienced by the wheel during the deceleration phase.