Question

Write the equation of a line that passes through the point (0, 3) and (-4, 11). *

Answer 1

`\large \boxed{y = - 2x + 3}`

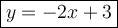
Explanation:

Goal

• Write the equation of a line with given coordinate points

Given

• Coordinate points which are (0,3) and (-4,11).

Step 1

• Use the slope formula also known as rise over run to calculate the slope.

`\large \boxed{m = (y_2-y_1)/(x_2-x_1) }`

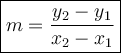
Substitute coordinate points in.

`m = (11 - 3)/( - 4 - 0) \\ m = (8)/( - 4) \longrightarrow (2)/( - 1) \\ m = - 2`

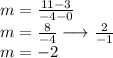
Step 2

• Substitute the value of slope in the slope-intercept form.

`\large \boxed{y = mx + b}`

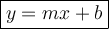
where m = slope and b = y-intercept.

`y = - 2x + b`

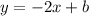
Step 3

• Substitute any given coordinate points in the new equation to find the value of b.

Substitute both coordinate points still give the same solution.

Step 3.1 — (0,3)

`y = - 2x + b \\ 3 = - 2(0) + b \\ 3 = 0 + b \\ 3 = b`

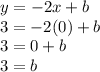
Step 3.2 — (-4,11)

`y = - 2x + b \\ 11 = - 2( - 4) + b \\ 11 - 8 = b \\ 3 = b`

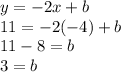
Therefore, the value of b is 3.

Step 4

• Substitute the value of b in the equation.

`y = - 2x + b \\ y = - 2x + 3`

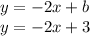
Hence, the equation of a line is y = -2x+3.