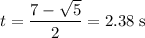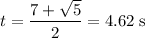Question

6) The height h(t) of a projectile is given by

h(t) = −t² + 7t + 9.
Find the time (s) at which the rocket is
20 ft above the ground.

Answer 1

2.38 s

4.62 s

Explanation:

The height of a projectile is given by the function:

`h(t) = -t^2 + 7t + 9`

where:

• h(t) is the height of the rocket about the ground (in feet).
• t is the time (in seconds).

To determine the time(s) at which the rocket is 20 ft above the ground, set h(t) = 20 and solve for t.

`-t^2+7t+9=20`

To solve the equation for t, complete the square.

Subtract 9 from both sides:

`-t^2+7t=11`

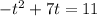
Divide both sides by -1:

`t^2-7t=-11`

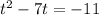
Add the square of half the coefficient of the term with the variable "t" to both sides of the equation:

`t^2-7t+\left((-7)/(2)\right)^2=-11+\left((-7)/(2)\right)^2`

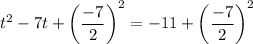
Simplify:

`t^2-7t+(49)/(4)=(5)/(4)`

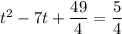
We have now created a perfect square trinomial on the left side of the equation. Factor the perfect square trinomial:

`\left(t-(7)/(2)\right)^2=(5)/(4)`

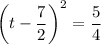
To solve for t, square root both sides:

`t-(7)/(2)=\pm \sqrt{(5)/(4)}`

`t-(7)/(2)=\pm(√(5))/(2)`

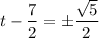
Add 7/2 to both sides of the equation:

`t=(7)/(2)\pm(√(5))/(2)`

`t=(7\pm√(5))/(2)`

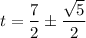
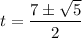
Therefore, the times at which the rocket is 20 ft above the ground is:

`t=(7-√(5))/(2)=2.38\; \rm s`

`t=(7+√(5))/(2)=4.62\; \rm s`