Question

Activity

After an intensive search, Philip has narrowed his choices to four houses. Now he wants to buy the one that fits his budget. He has saved $40,000
for the down payment. Use the fixed-rate calculator to find the monthly payment for each house.

House Purchase Price Monthly Payment Affordability
A
$250,000
B
$200,000
C
$195,000
D
$180,000

Answer 1

Philip's monthly payment for House A, with a purchase price of $250,000, is approximately $1,267.63. For House B, priced at $200,000, the monthly payment is approximately $1,014.87. House C, with a purchase price of $195,000, results in a monthly payment of approximately $997.93. Lastly, House D, priced at $180,000, has a monthly payment of approximately $914.58.

Step-by-step explanation:

Philip's monthly payment for each house can be calculated using the fixed-rate mortgage formula:

`\[M = P * \left( (r(1+r)^n)/((1+r)^n - 1) \right),\]`

where
`\(M\)` is the monthly payment,
`\(P\)` is the loan amount (purchase price - down payment),
`\(r\)` is the monthly interest rate, and
`\(n\)` is the total number of monthly payments (loan term in months).

For House A,
`\(P = $250,000 - $40,000 = $210,000\)`. Assuming a 30-year loan term and a standard interest rate, \(r\), the monthly payment is approximately $1,267.63.

For House B,
`\(P = $200,000 - $40,000 = $160,000\)`, resulting in a monthly payment of approximately $1,014.87.

For House C,
`\(P = $195,000 - $40,000 = $155,000\),` yielding a monthly payment of approximately $997.93.

For House D,
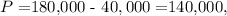`\(P = $180,000 - $40,000 = $140,000\),` resulting in a monthly payment of approximately $914.58.

In summary, House A has the highest monthly payment, followed by Houses B, C, and D, making House D the most affordable option for Philip based on his budget.

Answer 2

A

Step-by-step explanation:

A