Question

Which factor could be multiplied by the given function so that their product causes the graph of f(x) to decrease as x approaches negative infinity?


`f(x)=(2x^2 + 5)(x - 7)`

Select all that apply.

• -3
• 0.2x
• 5x²
•
`-(1)/(2)(x + 8)`
• 4(2x - 7)

Answer 1

3rd and 4th Choices.

`\displaystyle 5x^2\text{ and } -(1)/(2)(x+8)`

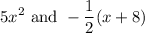
Explanation:

We are given the function:

`f(x)=(2x^2+5)(x-7)`

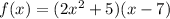
And we want to determine the factor(s) that we can multiply to the above function that will cause the graph of f to decrease as x approaches negative infinity.

We can see that the dominant term will be:

`2x^2(x)=2x^3`

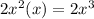
Thus:

`2(-\infty)^3\Rightarrow -\infty`

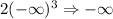
It is already decreasing (shifting towards negative infinity) as x approaches negative infinity.

In order to preserve this, then, the factors must be positive as x approaches negative infinity.

The first factor is -3.

-3 is always negative, so it will make f increase.

The second factor is
`0.2x`.

`0.2(-\infty)\Rightarrow -\infty`

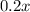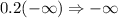
This will also make f increase.

The third factor is:

`5(\infty)^2\Rightarrow \infty`

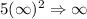
This is positive, so it will allow f to remain decreasing as x approaches negative infinity.

The fourth factor is:

`\displaystyle -(1)/(2)(-\infty+8)\Rightarrow -(1)/(2)(-\infty)\Rightarrow \infty`

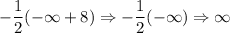
This is also positive, so it will also allow f to remain decreasing.

Lastly, the fifth factor is:

`4(2(-\infty)-7)\Rightarrow 4(-\infty)\Rightarrow -\infty`

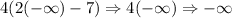
This is negative, so it will make f increasing.

Therefore, our answers are the third and fourth choices.

Answer 2

5x²

-1/2( x+8)

Explanation:

The dominant term is 2x^2 *x or 2x^3

We want to know what happens when x goes to negative ∞

2 ( -∞) ^3 → 2 * (-∞) → -∞

As long as we multiply by a positive number, we will still be approaching negative infinity ( or decreasing)

-3 is negative

.2x is negative when x approaches negative infinity

.5 x^2 = .5( -∞)^2 = 5 ( ∞) = ∞ which is positive

-1/2 x is the dominant term = -1/2(- ∞) = ∞ which is positive

4(2x) is the dominant term = 8(- ∞) = - ∞ which is negative