a) The moment of inertia (l) of the turntable about the rotation axis is approximately
 .
.
b) If the workshop makes this turntable in the shape of a uniform solid disk, its mass (m) should be approximately
 .
.
a. Given:
Kinetic energy (KE) = 0.270 J
Angular velocity
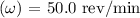
First, convert the angular velocity from rev/min to rad/s:
![\[\omega = \frac{2\pi * \text{revolutions}}{60 \, \text{s}} * \text{rev/min}\]](https://img.qammunity.org/2024/formulas/physics/high-school/ctl2aa4bpyf4hxwl3r9m212m6tlnhees1l.png)
![\[\omega = (2\pi * 50.0)/(60) \, \text{rad/s}\]](https://img.qammunity.org/2024/formulas/physics/high-school/oqqgs4g9lj4vmeds80knejfroz3kp9gsfn.png)
![\[\omega = (5\pi)/(6) \, \text{rad/s}\]](https://img.qammunity.org/2024/formulas/physics/high-school/sspr6sp1o3amqhr9owrqp2hij01rn4r09j.png)
Now, calculate the moment of inertia (I) using the formula:
![\[ I = (2KE)/(\omega^2)\]](https://img.qammunity.org/2024/formulas/physics/high-school/cw7a8eptvuqqn6ihc0n6zwk3q0b4qp7h7l.png)
![\[ I = \frac{2 * 0.270 \, \text{J}}{\left((5\pi)/(6)\right)^2}\]](https://img.qammunity.org/2024/formulas/physics/high-school/4m5oqjpqq8r9rsancxr2zonjz4iuc1ibv3.png)
![\[ I = \frac{2 * 0.270 \, \text{J}}{\left((25\pi^2)/(36)\right)}\]](https://img.qammunity.org/2024/formulas/physics/high-school/449njsvg5hopluyk31ivxeubh9y5k1j8h4.png)
![\[ I = (0.540)/(25\pi^2/36)\]](https://img.qammunity.org/2024/formulas/physics/high-school/rrgi2tujxs7b4kr4zh7k1s48qcf5kx8awh.png)
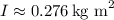
This is the moment of inertia (I) of the turntable.
Now, for the mass (m) of the uniform solid disk:
b. Given:
Diameter (d) = 45.0 cm
Radius (r)
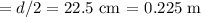
The formula for the moment of inertia (I) of a uniform solid disk is
Rearrange the formula to solve for the mass (\(m\)):
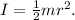
![\[ m = (2I)/(r^2)\]](https://img.qammunity.org/2024/formulas/physics/high-school/8xt09prcggp5pfliajghnrxzoqlydzvtak.png)
![\[ m = \frac{2 * 0.276 \, \text{kg m}^2}{(0.225 \, \text{m})^2}\]](https://img.qammunity.org/2024/formulas/physics/high-school/ncyi7dzfx4gdlvzr9jur2vhnqsgy70vizr.png)
![\[ m = (0.552)/(0.050625) \, \text{kg}\]](https://img.qammunity.org/2024/formulas/physics/high-school/wkqgigprp3284i6xfrn1iksj0rywcdv7go.png)
![\[ m \approx 10.89 \, \text{kg}\]](https://img.qammunity.org/2024/formulas/physics/high-school/sczyejvdgmxel9nx8ieo2bucf1k9fk0zex.png)
Therefore, the mass of the uniform solid disk that forms the turntable would be approximately 10.89 kg.