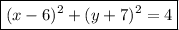Question

NO LINKS!!! URGENT HELP PLEASE!!!

Determine the equation of the circle graphed below.

Answer 1

`(x-6)^2+(y+7)^2=4`

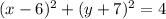
Explanation:

The formula for the equation of a circle is:

`\boxed{(x-h)^2+(y-k)^2=r^2}`

where:

• (h, k) is the center.
• r is the radius.

From inspection of the given graphed circle, we can see that the coordinates of its center are (6, -7), and its radius is 2 units. Therefore:

• h = 6
• k = -7
• r = 2

To determine the equation of the graphed circle, substitute these values into the equation of a circle formula:

`\implies (x-6)^2+(y-(-7))^2=2^2`

`\implies (x-6)^2+(y+7)^2=4`

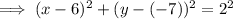
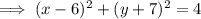
Therefore, the equation of the graphed circle is:

`\boxed{(x-6)^2+(y+7)^2=4}`