Question

Can you guys help me do thus

Answer 1

(a) x = 6.71 cm (3 s.f.)

θ = 30.8° (3 s.f.)

(b) radius = 3.00 cm (3 s.f.)

Explanation:

Part (a)

The given triangle is made up of two right triangles.

In the right triangle on the right side, the side labelled "x" is opposite angle 40° and the side labelled 8 cm is adjacent to angle 40°. Therefore, to find the length of side x, use the tangent trigonometric ratio.

`\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}`

Therefore, the values are:

• θ = 40°
• O = x
• A = 8 cm

Substitute the values into the equation and solve for x:

`\implies \tan 40^(\circ)=(x)/(8)`

`\implies 8 \cdot \tan 40^(\circ)=8 \cdot(x)/(8)`

`\implies 8 \tan 40^(\circ)=x`

`\implies x=8 \tan 40^(\circ)`

`\implies x=6.71279704...`

`\implies x=6.71\; \rm cm\;(3\;s.f.)`

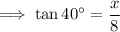
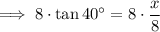
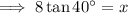
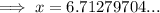
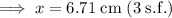
Therefore, the length of side x is 6.71 cm (3 s.f.).

In the right triangle on the left side, the side labelled "x" is adjacent angle θ and the side labelled 4 cm is opposite to angle θ. Therefore, to find the size of angle θ, use the tangent trigonometric ratio.

Therefore, the values are:

• θ = θ
• O = x
• A = 4 cm

Substitute the values into the equation and solve for x:

`\implies \tan \theta=(4)/(x)`

`\implies \tan \theta=(4)/(8 \tan 40^(\circ))`

`\implies \tan \theta=(1)/(2 \tan 40^(\circ))`

`\implies \theta=\tan^(-1)\left((1)/(2 \tan 40^(\circ))\right)`

`\implies \theta=30.7897330...^(\circ)}`

`\implies \theta=30.8^(\circ)}\; \rm (3\;s.f.)`

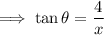
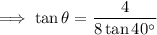
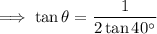
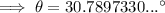
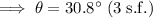
Therefore, the size of angle θ is 30.8° (3 s.f.).

`\hrulefill`

Part (b)

The formula for the volume of a cylinder is:

`\boxed{V=\pi r^2 h}`

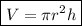
where:

• V is the volume.
• r is the radius.
• h is the height.

Given values:

• height, h = 5.3 cm
• volume, V = 150 cm³

Substitute the given values into the formula and solve for r:

`\implies \pi \cdot r^2 \cdot 5.3 = 150`

`\implies r^2=(150)/(5.3\pi)`

`\implies √(r^2)=\sqrt{(150)/(5.3\pi)}`

`\implies r=√(9.00877036...)`

`\implies r=3.00146137...`

`\implies r=3.00\; \rm cm\;(3\;s.f.)`

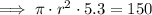
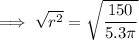
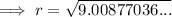
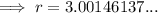
Therefore, the radius of the cylinder is 3.00 cm (3 s.f.)