Question

Find the value of a
Answer is 3

Answer 1

Explanation:

Use the Ratio Test since Ratio Test guarantee absolutely convergence.

`\frac{ ( - 1) {}^(k + 1)(k + 1) {}^(a) }{5 {}^(k + 1)(3(k + 1) } * \frac{5 {}^(k)(3k) }{(k) {}^(a) ( - 1) {}^(k) }`

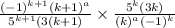
This simplifes to

`\frac{( - 1) {}^(k) ( - 1) ((k + 1)!) {}^(a) }{5 {}^(k)(5)(3k +1) ! } * \frac{5 {}^(k) (3k)!}{( - 1) {}^(k) (k!) {}^(a) }`

`\frac{ - (k + 1) {}^(a) }{5(3k + 3)(3k + 2)(3k + 1)}`

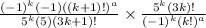
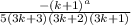
Take the absolute value

`\frac{(k + 1) {}^(a) }{5(3k + 3)(3k + 2)(3k + 1)}`

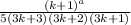
In order for this series to be convergent,

the limit as k approaches infinity must be less than 1.

In order for this series to have a limit less than 1, our numerator and denominator degree must be equal or the denominator must have the larger degree.

Why

If the numerator has a larger degree, our test would make this divergent, so the limit would be infinity

Since the denominator have 3 binomials, our power for the denominator will be 3, this the numerator having a degree of 3 or less as well.

So one of the answer is 3.