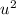Question

Please Factorise 4u²-18u +18 ​

Answer 1

Answer: 2(u-3)(2u-3)

Explanation:

4u²-18u +18 take out the greatest common factor, 2, all terms can be divided by 2

2(2u²-9u +9) to factor, multiply the first and the last parts of the quadratic. 2(9)=18 Find 2 numbers that multiply to 18 but add to the middle number.

-6 and -3 both multyiply to +18 but add to -9

Take those 2 numbers, -6 and -3, and replace the middle term with those numbers

2(2u²-6u-3u +9) we have not changed the equation, we have simply replaced the term and broke it up. -9u = -6u-3u

2(2u²-6u-3u+9) now we "group" the first 2 terms and the last 2

2[(2u²-6u)(-3u +9)] this is not your factor you must take out the greatest common factor from each of the groupings

2[2u(u-3)-3(u-3)] if the parentheses are the same, then you've done a good job. the first factoring will be what is in your parentheses, the second will be what ever is left.

2(u-3)(2u-3)

We use this method because there is a coefficient, number in front of the
`u^(2)`

Answer 2

To factorise 4u²-18u +18, we can start by factoring out the greatest common factor, which is 2:

2(2u² - 9u + 9)

Next, we can try to factor the quadratic expression inside the parentheses. We can use the quadratic formula to find the roots of the expression:

u = [9 ± sqrt(9² - 4(2)(9))]/(2(2))

Simplifying the expression, we get:

u = [9 ± 3sqrt(2)]/4

Therefore, the factors of 4u²-18u +18 are:

2(2u - 3 + sqrt(2))(u - 3 - sqrt(2))