Question

Decide if each set of numbers represents a Pythagorean triple

9. 5,12,13
10. 10,17,24
11. 7,14,7 square root of 5

Answer 1

9. yes

10. no

11. yes

Explanation:

A Pythagorean triple are 3 numbers that work out to be sides of a right triangle, for which we use the Pythagorean theorem, a^2 + b^2 = c^2.

"a" and "b" are the legs of the triangle, and "c" is the hypotenuse, which is the longest side.

For problem 9, we can plug in 5^2 + 12^2 = 13^2 and see if it's true. If it is true, those numbers are a Pythagorean triple. If it is false, than they are not.

9. 5^2 + 12^2 13^2 = 169

25 + 144 = 169

Squaring the legs and adding them come up with 169, which is "c" squared, the hypotenuse, or longest leg, 13. So, take the square root of 169, the answer of the left side of the equation, and we see that it works out.

10. 10^2 + 17^2 = 24^2 24^2 = 576

100 + 289 = 289

After doing the left side of the equation by squaring the shorter numbers, those add up to 289. The hypotenuse squared (24^2) = 576, which is not 289, so this set of numbers are not a Pythagorean triple

11. Here, you need to figure out what number 7
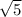`√(5)` is to see if it's a leg or hypotenuse. I like to make it all into a square root of a number (desymplifying it) first. the 7 comes from a perfect square root,
`√(49)`, so we can multiply these numbers under the radical sign to equal
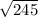`√(245)` which equals about 15.65, so it is the hypotenuse ("c") because it is the largest number.

7^2 + 14^2 (7
`√(5)`)^2 =
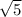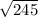`√(245)`^2 = 245

49 + 196 = 245

245 = 245

a^2 + b^2 = c^2 works out for this equation so it is a Pythagorean triple.