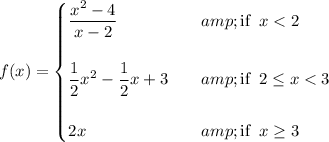Solve for a and b so that f(x) is continuous at all points. f(x) = \begin{cases}(x^2-4)/(x-2) & \text{if } x\ \textless \ 2 \\ax^2-bx+3 & \text{if } 2\le x \ \textless \…

Question

Solve for a and b so that f(x) is continuous at all points.


`f(x) = \begin{cases}(x^2-4)/(x-2) & \text{if } x\ \textless \ 2 \\ax^2-bx+3 & \text{if } 2\le x \ \textless \ 3\\2x-a+b & \text{if } x\ge 3\end{cases}`

Answer 1

`a=(1)/(2),\;\;b=(1)/(2)`

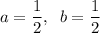
Explanation:

A function f is continuous at x = a when:

`\bullet\quad\textsf{$f(a)$\;is\;d\:\!efined.}`

`\bullet\quad\textsf{$\displaystyle \lim_(x \to a) f(x)$\;exists.}`

`\bullet\quad\displaystyle \lim_(x \to a) f(x) = f(a)`

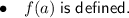
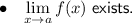
To ensure that f(x) is continuous at x = 2 and x = 3, we need to make sure that the limit of f(x) as x approaches 2 from the left is equal to the limit of f(x) as x approaches 2 from the right, and similarly for x = 3.

First, factor the numerator and simplify the rational function:

`f(x)=(x^2-4)/(x-2)=((x+2)(x-2))/(x-2)=x+2`

As x approaches 2 from the left, x < 2. Therefore, to find the limit as x approaches 2 from the left, substitute x = 2 into the first sub-function:

`\displaystyle \lim_(x \to 2^(-)) f(x)=2+2=4`

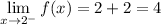
As x approaches 2 from the right, x > 2. Therefore, to find the limit as x approaches 2 from the right, substitute x = 2 into the second sub-function:

`\begin{aligned}\displaystyle \lim_(x \to 2^(+)) f(x)&=a(2)^2-b(2)+3\\&=4a-2b+3\end{aligned}`

To ensure continuity at x = 2, equate the limits:

`4=4a - 2b + 3`

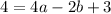
Solve for b in terms of a:

`\begin{aligned}4&=4a - 2b + 3&\\ 2b+4&=4a+3\\2b&=4a-1\\b&=2a-(1)/(2)\end{aligned}`

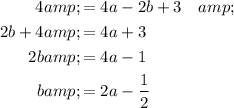
Now, we need to find a and b so that f(x) is continuous at x = 3.

As x approaches 3 from the left, x < 3. Therefore, to find the limit as x approaches 3 from the left, substitute x = 3 into the second sub-function:

`\begin{aligned}\displaystyle \lim_(x \to 3^(-)) f(x)&=a(3)^2 - b(3) + 3\\&= 9a - 3b + 3\end{aligned}`

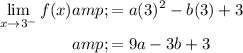
As x approaches 3 from the right, x > 3. Therefore, to find the limit as x approaches 3 from the right, substitute x = 3 into the third sub-function:

`\begin{aligned}\displaystyle \lim_(x \to 3^(+)) f(x)&= 2(3) - a + b\\&= 6 - a + b\end{aligned}`

To ensure continuity at x = 3, equate the limits:

`9a - 3b + 3 = 6-a+b`

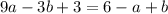
Solve for b in terms of a:

`\begin{aligned}9a - 3b + 3 &= 6-a+b\\10a-3b+3&=6+b\\10a+3&=6+4b\\10a-3&=4b\\4b&=10a-3\\b&=(5)/(2)a-(3)/(4)\end{aligned}`

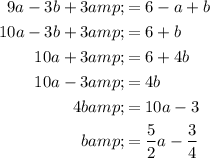
Substitute this expression for b into the equation obtained from continuity at x = 2:

`(5)/(2)a-(3)/(4)=2a-(1)/(2)`

Solve for a:

`\begin{aligned}(5)/(2)a-(3)/(4)&=2a-(1)/(2)\\\\(1)/(2)a-(3)/(4)&=-(1)/(2)\\\\(1)/(2)a&=(1)/(4)\\\\a&=(1)/(2) \end{aligned}`

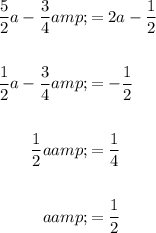
Substitute the found value of a into the expression for b and solve for b:

`\begin{aligned}b&=2\left((1)/(2)\right)-(1)/(2)\\b&=1-(1)/(2)\\b&=(1)/(2)\end{aligned}`

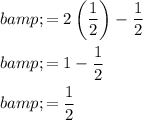
Therefore, the values of a and b that make f(x) continuous at all points are:

`a=(1)/(2),\;\;b=(1)/(2)`

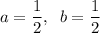
So the function f(x) is:

`f(x)=\begin{cases} (x^2-4)/(x-2)&\text{if}\;\;x < 2\\\\(1)/(2)x^2-(1)/(2)x+3\quad&\text{if}\;\;2 \leq x < 3\\\\2x&\text{if}\;\;x \geq 3\end{cases}`