Question

Solve the equation for 0 ≤ x < 2π

Answer 1

x ∈ {π/4, π/3, 2π/3, 3π/4}

Explanation:

You want the solutions on the interval [0, 2π) of the equation ...

`-4\cos^2(x)-2(√(3)+√(2)\sin(x)+√(6)+4=0`

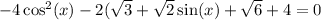
Identity

Replacing the cosine function with its equivalent, we have a quadratic in sin(x).

`-4(1-\sin^2(x))-2(√(3)+√(2)\sin(x)+√(6)+4=0\\\\4\sin^2(x)-2(√(3)+√(2))\sin(x)+√(6)=0\\\\(2\sin(x)-√(3))(2\sin(x)-√(2))=0\\\\x\in\left\{(\pi)/(2)\pm(\pi)/(4),(\pi)/(2)\pm(\pi)/(6)\right\}\\\\\boxed{x\in\left\{(\pi)/(4),(\pi)/(3),(2\pi)/(3),(3\pi)/(4)\right\}}`

__

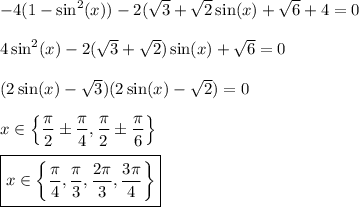
Additional comment

It is helpful to have the solutions provided by a graphing calculator. This gives a useful clue as to how the equation factors.

The graph was created using Desmos.

<95141404393>