Question

A total of $7000 is invested: part at 7% and the remainder at 12%. How much is invested at each rate if the annual interest is $650?

Answer 1

3800 invested at 7%; 3200 invested 12%

Explanation:

We will need a system of equations to solve for the interest invested at both interest rates.

We can allow x to represent the amount invested at 7% and y to represent the amount invested at 12%.

We know that the amount invested at 7% + the amount invested at 12% = total investment

Thus, our first equation is x + y = 7000

We further know that the interest earned at 7% + the interest earned at 12% = total interest earned

Since we calculate interest by multiplying the investment and the interest rate, our other equation is 0.07x + 0.12y = 650 (we had to convert the percentages to decimals for the sake of the problem)

We can solve first for y by isolating x in the first equation and plugging it in for y in the second equation:

`x+y=7000\\x=-y+7000\\\\0.07(-y+7000)+0.12y=650\\-0.07y+490+0.12y=650\\0.05y+490=650\\0.05y=160\\y=3200`

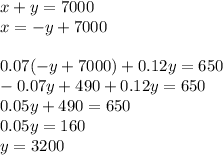
Now that we've found y, we can solve for x using any of the two equations, although the equation with no coefficients is much simpler:

`x+3200=7000\\x=3800`

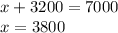
Now, we can check by plugging in 3800 for x and 3200 for y in both equations:

First equation

3800 + 3200 = 7000

7000 = 7000

Second equation

0.07(3800) + 0.12(3200) = 650

266 + 384 = 650

650 = 650