Question

A ball is thrown from an initial height of 2 meters with an initial upward velocity of 13 m/s. The ball's height / (in meters) after t seconds is given by the

following.
h=2+13t-5t^2
Find all values of t for which the ball's height is 9 meters.
Round your answer(s) to the nearest hundredth.
(If there is more than one answer, use the "or" button)

Answer 1

so we'd want to find all "t" when the ball was 9 meters up in the air, or namely what's "t" when h(t) = 9, well, let's simply set h(t) = 9

`\stackrel{h(t)}{9}=2+13t-5t^2\implies 0=-5t^2+13t-7 \\\\[-0.35em] ~\dotfill\\\\ ~~~~~~~~~~~~\textit{quadratic formula} \\\\ 0=\stackrel{\stackrel{a}{\downarrow }}{-5}t^2\stackrel{\stackrel{b}{\downarrow }}{+13}t\stackrel{\stackrel{c}{\downarrow }}{-7} \qquad \qquad t= \cfrac{ - b \pm \sqrt { b^2 -4 a c}}{2 a}`

`t= \cfrac{ - (13) \pm \sqrt { (13)^2 -4(-5)(-7)}}{2(-5)} \implies t = \cfrac{ -13 \pm \sqrt { 169 -140}}{ -10 } \\\\\\ t= \cfrac{ -13 \pm \sqrt { 29 }}{ -10 }\implies t= \begin{cases} \frac{ -13 + \sqrt { 29 }}{ -10 }\\\\ \frac{ -13 - \sqrt { 29 }}{ -10 } \end{cases}\implies t\approx \begin{cases} 0.76\\\\ 1.84 \end{cases} ~~ \textit{\LARGE seconds}`

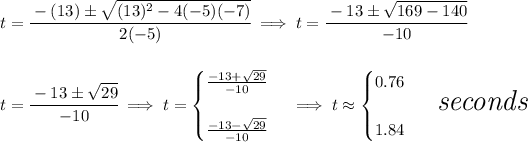
there are two values, Check the picture below, that's about the parabolic path for the object, and it hits 9 meters high twice, once on the way up, and again on the way down.