Given:
The variable y varies directly as x and inversely as z. When x = 4 and z= 14, y=2.
To find:
The combined variation equation and find y when x = 6 and z= 3.
Solution:
The variable y varies directly as x and inversely as z.
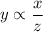
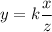 ...(i)
...(i)
Where, k is the constant of proportionality.
Putting x=4, y=2 and z=14, we get
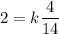
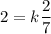
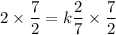
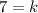
Putting k=7 in (i), we get
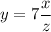
Putting x=6 and z=3, we get
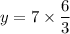
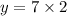
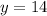
Therefore, the required equation is
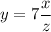 and the value of y is 14 when x = 6 and z= 3.
and the value of y is 14 when x = 6 and z= 3.