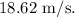Question

A ball punted vertically has a hang time of 3.8 seconds.

A. Construct position-time, velocity-time, and acceleration-time graphs and a motion map for this situation.
B. What was its initial velocity?

Answer 1

A.

Position-time graph:

The position-time graph for the ball punted vertically will be a parabolic curve, with the vertex at the highest point of the ball's trajectory. Since the initial position is zero, the curve will go through the origin.

Velocity-time graph:

The velocity-time graph will be a straight line that starts at the initial velocity and decreases linearly until it reaches zero at the highest point of the ball's trajectory. After that, the velocity increases linearly in the negative direction until the ball hits the ground.

Acceleration-time graph:

The acceleration-time graph will be a constant negative value, representing the acceleration due to gravity.

Motion map:

A motion map is a diagram that shows the position of an object at several specific times during its motion. For the ball punted vertically, the motion map would look like this:

|O|------|-------|------|-------|------|H|

O represents the initial position, and H represents the highest point of the ball's trajectory. The "|" symbols represent the position of the ball at regular intervals of time.

B.

To find the initial velocity of the ball, we can use the hang time and the acceleration due to gravity.

Hang time = 3.8 seconds

Acceleration due to gravity = -9.8 m/s^2

At the highest point of the ball's trajectory, the velocity is zero. Therefore, we can use the following kinematic equation to find the initial velocity:

hang time = (final velocity - initial velocity) / acceleration

Solving for initial velocity:

initial velocity = final velocity - (hang time x acceleration)

final velocity = 0 m/s

hang time = 3.8 s

acceleration = -9.8 m/s^2

initial velocity = 0 - (3.8 x -9.8)

initial velocity = 37.64 m/s

Therefore, the initial velocity of the ball was 37.64 m/s.

Answer 2

A. For a ball punted vertically, position-time graph is a downward-opening parabola, velocity-time graph is linear, and acceleration-time graph is a horizontal line. Motion map shows upward and downward motion. B. Initial velocity is approximately
`\(18.62 \ m/s\).`

Let's break down the problem step by step:

A. Construct position-time, velocity-time, and acceleration-time graphs, and a motion map:

1. Position-time graph (s-t):

- The position-time graph for an object in free fall (assuming no air resistance) would be a quadratic function with the equation
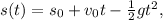`\(s(t) = s_0 + v_0t - (1)/(2)gt^2\),` where:

- \(s(t)\) is the position at time \(t\),

- \(s_0\) is the initial position (which we can assume to be 0 for simplicity),

-
`\(v_0\)` is the initial velocity,

-
`\(g\)` is the acceleration due to gravity (approximately
`\(9.8 \ m/s^2\)),`

-
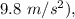
`\(t\)` is time.

2. Velocity-time graph (v-t):

- The velocity-time graph will be a linear function. The slope of this line represents the acceleration due to gravity.

3. Acceleration-time graph (a-t):

- The acceleration is constant and equal to \(g\), so the acceleration-time graph will be a horizontal line at
`\(9.8 \ m/s^2\).`

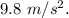
4. Motion map:

- A motion map is a series of images or drawings that represent the position of the object at different points in time. Since the ball is punted vertically, the motion map will show the ball going up and then coming back down. the motion map would look like this:

|O|------|-------|------|-------|------|H|

B. Calculate the initial velocity
`(\(v_0\)):`

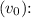
- The hang time is the total time the ball is in the air, which is the sum of the time it takes to reach the highest point and the time it takes to come back down. The time to reach the highest point is half of the total hang time.

`\[ t_{\text{up}} = \frac{\text{hang time}}{2} \]`

`\[ v_0 = g \cdot t_{\text{up}} \]`

Now, let's calculate:

`\[ t_{\text{up}} = \frac{3.8 \ \text{seconds}}{2} = 1.9 \ \text{seconds} \]`

`\[ v_0 = (9.8 \ \text{m/s}^2) \cdot (1.9 \ \text{seconds}) \]`

`\[ v_0 = 18.62 \ \text{m/s} \]`

So, the initial velocity of the ball is approximately
`\(18.62 \ \text{m/s}\).`