Question

How many liters of water can be made from 155 grams of oxygen gas and an excess of hydrogen at 0.850 atm and 310K?

___H2(g) + ___O2(g) = ___H₂O(g)

Answer 1

290 L (3 s.f.)

Step-by-step explanation:

First, balance the equation:

2H₂(g) + O₂(g) → 2H₂O(g)

Now, calculate the number of moles in the given mass of oxygen gas (O₂) by using the formula:

`\boxed{n = (m)/(M)}`

where:

• n is the number of moles.
• m is the mass (in grams).
• M is the molar mass of the material.

The molar mass of O₂ is 31.999 g/mol.

Therefore, the number of moles in 155 g of oxygen gas is:

`\rm (155\;g)/(31.999\;g/mol)=4.844\; \rm mol\;(3\;d.p.)`

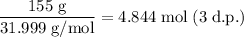
We have been told that hydrogen is in excess, which means we can assume that all the moles of oxygen will react.

The mole ratio between oxygen gas and water is 1 : 2. This means that the reaction will produce twice as many moles of water as moles of oxygen. Therefore, the number of moles of water is:

`\rm 4.844* 2=9.688\; \rm mol\;(3\;d.p.)`

To determine how many liters of water can be made at 0.850 atm and 310 K, use the ideal gas law equation.

Ideal Gas Law

`\boxed{PV=nRT}`

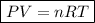
where:

• P is the pressure measured in atmosphere (atm).
• V is the volume measured in liters (L).
• n is the number of moles.
• R is the ideal gas constant (0.082057366080960 atm L mol⁻¹ K⁻¹).
• T is the temperature measured in kelvin (K).

Rearrange the formula to isolate V:

`\implies V=(nRT)/(P)`

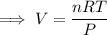
Substitute the values into the formula and solve for V:

`\implies V=\rm (9.688\;mol \cdot 0.082057... atm\;L\;mol^(-1)\;K^(-1) \cdot 310\;K)/(0.850\;atm)`

`\implies V=\rm (9.688\cdot 0.082057...\;L \cdot 310)/(0.850)`

`\implies V=\rm 289.930...\;L`

`\implies V=\rm290\;L\;(3\;s.f.)`

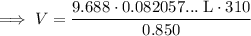
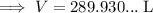
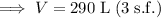
Therefore, 290 liters of water (to three significant figures) can be made from 155 grams of oxygen gas and an excess of hydrogen at 0.850 atm and 310 K.