Question

The speed of an electron is known to be between 3.0×10^6 m/s and 3.3×10^6 m/s . Estimate the uncertainty in its position.

Answer 1

Approximately
`3.9* 10^(-11)\; {\rm m}`.

Step-by-step explanation:

By the Heisenberg Uncertainty Principle:

`\displaystyle \Delta p\, \Delta x \ge (h)/(4\, \pi)`,

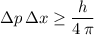Where:

• 
  `\Delta p` is the uncertainty in momentum,
• 
  `\Delta x` is the uncertainty in position, and
• 
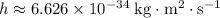  `h \approx 6.626 * 10^(-34)\; {\rm kg \cdot m^(2)\cdot s^(-1)}` is Planck's Constant.

In this question, the measured velocity of this electron is
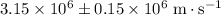`3.15 * 10^(6) \pm 0.15* 10^(6)\; {\rm m\cdot s^(-1)}`. The uncertainty of this measurement is
`\Delta v = 1.5 * 10^(5)\; {\rm m\cdot s^(-1)}`.

Assume that the mass of this electron is the same as that of a stationary electron:
`m = m_(e) \approx 9.11 * 10^(-31)\; {\rm kg}`.

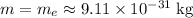With an uncertainty in velocity of
`\Delta v = 1.5 * 10^(5)\; {\rm m\cdot s^(-1)}`, the uncertainty in the momentum of this electron would be:

`\begin{aligned}\Delta p &= m\, \Delta v \\ &\approx (9.11 * 10^(-31)\; {\rm kg})\, (1.5 * 10^(5)\; {\rm m\cdot s^(-1)}) \\ &\approx 1.3665 * 10^(-24)\; {\rm kg\cdot m\cdot s^(-1)} \end{aligned}`.

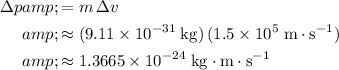Rearrange the Uncertainty Principle to find the uncertainty in position:

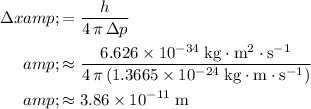`\begin{aligned}\Delta x &= (h)/(4\, \pi\, \Delta p) \\ &\approx \frac{6.626 * 10^(-34)\; {\rm kg\cdot m^(2)\cdot s^(-1)}}{4\, \pi\, (1.3665 * 10^(-24)\; {\rm kg\cdot m\cdot s^(-1)})} \\ &\approx 3.86 * 10^(-11)\; {\rm m}\end{aligned}`.